题目内容
【题目】如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于G.则下列结论中错误的是( ) 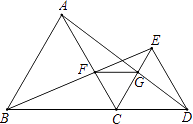
A.AD=BE
B.BE⊥AC
C.△CFG为等边三角形
D.FG∥BC
【答案】B
【解析】解:A、∵△ABC和△CDE均为等边三角形,
∴AC=BC,EC=DC,
∠ACB﹦∠ECD=60°,
∴∠ACD﹦∠ECB,
在△ACD与△BCE中,
∵  ,
,
∴△ACD≌△BCE(SAS),
∴AD=BE,正确,故本选项错误;
B、根据已知不能推出F是AC中点,即AC和BF不垂直,所以AC⊥BE错误,故本选项正确;
C、△CFG是等边三角形,理由如下:
∵∠ACG=180°﹣60°﹣60°=60°=∠BCA,
∵△ACD≌△BCE,
∴∠CBE=∠CAD,
在△ACG和△BCF中
∵ 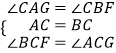 ,
,
∴△ACG≌△BCF(ASA),
∴CG=CH,
又∵∠ACG=60°
∴△CGH是等边三角形,正确,故本选项错误;
D、∵△CFG是等边三角形,
∴∠CFG﹦60°=∠ACB,
∴FG∥BC,正确,故本选项错误;
故选B.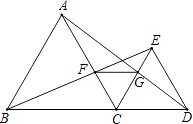
A、证明△ACD≌△BCE即可得出答案;
B、根据等边三角形性质得出AB=BC,只有F为AC中点时,才能推出AC⊥BE.
C、由△ACG≌△BCF,推出CG=CF,根据∠ACG=60°即可证明;
D、根据等边三角形性质得出∠CFG﹦∠ACB=60°,根据平行线的判定推出即可.

练习册系列答案
相关题目