题目内容
已知二次函数y＝x2－x＋，当自变量x取m时，对应的函数值小于0，当自变量x取m－1、m＋1时，对应的函数值为y1、y2，则y1、y2满足
| A．y1＞0，y2＞0 | B．y1＜0，y2＞0 | C．y1＜0，y2＜0 | D．y1＞0，y2＜0 |
A
解析解：令y=x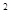
-x+
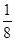=0，
解得：x=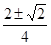
．
∵当自变量x取m时对应的值小于0，
∴
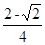＜m＜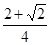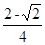
，
∴m-1＜ ，m+1＞ ，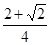
∴y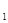
＞0，y
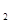＞0．
故选：A．点评：此题考查了抛物线与x轴的交点和二次函数图象上的点的特征，解题的关键是求得抛物线与横轴的交点坐标．
练习册系列答案
能考试全能100分系列答案
相关题目