题目内容
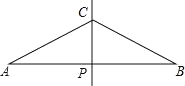
【题目】如图，AB的中垂线为CP交AB于点P，且AC=2CP．甲、乙两人想在AB上取D、E两点，使得AD=DC=CE=EB，其作法如下：甲作∠ACP、∠BCP的角平分线，分别交AB于D、E两点，则D、E即为所求；乙作AC、BC的中垂线，分别交AB于D、E两点，则D、E即为所求．对于甲、乙两人的作法，下列正确的是（ ）
A．两人都正确 B．两人都错误
C．甲正确，乙错误 D．甲错误，乙正确
【答案】A．
【解析】
试题解析：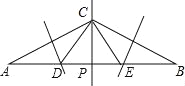
甲、乙都正确，
理由是：∵CP是线段AB的垂直平分线，
∴BC=AC，∠APC=∠BPC=90°，
∵AC=2CP，
∴∠A=30°，
∴∠ACP=60°，
∵CD平分∠ACP，
∴∠ACD=
∠ACP=30°，
∴∠ACD=∠A，
∴AD=DC，
同理CE=BE，
即D、E为所求；
∵D在AC的垂直平分线上，
∴AD=CD，
同理CE=BE，
即D、E为所求，
故选A．
练习册系列答案
名校课堂系列答案
相关题目
