题目内容
(2000•金华)如图,在矩形ABCD中,M是BC上一动点,DE⊥AM,E为垂足,3AB=2BC,并且AB,BC的长是方程x2-(k-2)x+2k=0的两个根,(1)求k的值;
(2)当点M离开点B多少距离时,△AED的面积是△DEM面积的3倍?请说明理由.

【答案】分析:(1)根据根与系数的关系,列出方程组解答;
(2)根据(1)中k的值解方程,求出AD和BC的长,然后根据相似三角形的性质解答.
解答:解:(1)根据题意列方程组得: 解得
解得 ,
,
即3k2-37k+12=0,解得k=12或k= .
.
(2)把k=12或k= 分别代入方程x2-(k-2)x+2k=0中,
分别代入方程x2-(k-2)x+2k=0中,
当k=12时原方程可化为x2-10x+24=0,
解得x=4或x=6,
∵3AB=2BC,∴AB=4,BC=6.
当k= 时原方程可化为x2+
时原方程可化为x2+ x+
x+ =0,解得x=-
=0,解得x=- 或x=-1(不合题意舍去).
或x=-1(不合题意舍去).
故AB=4,BC=6,
∵△AED的面积是△DEM的高相同,
∴△AED的面积是△DEM面积的3倍则AE=3ME,设
ME=x,则AE=3x,设BM=y.
在Rt△AED与Rt△MBA中,∵∠ABM=∠AED=90°,∠AMB=∠DAE,故两三角形相似,
由勾股定理得AB2+BM2=16x2----①,解得BM= ,
,
即 =
= ,即
,即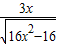 =
= ----②,
----②,
整理得x4-4x2+4=0,解得x2=2,x=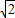 .
.
于是BM= =
= =4.
=4.
当点M离开点B的距离为4时,△AED的面积是△DEM面积的3倍.
点评:此题将动点问题与一元二次方程和矩形的性质相结合,通过相似三角形和同高不等底的三角形的性质,将面积关系转化为线段的性质解答.
(2)根据(1)中k的值解方程,求出AD和BC的长,然后根据相似三角形的性质解答.
解答:解:(1)根据题意列方程组得:
 解得
解得 ,
,即3k2-37k+12=0,解得k=12或k=
 .
.(2)把k=12或k=
 分别代入方程x2-(k-2)x+2k=0中,
分别代入方程x2-(k-2)x+2k=0中,当k=12时原方程可化为x2-10x+24=0,
解得x=4或x=6,
∵3AB=2BC,∴AB=4,BC=6.
当k=
 时原方程可化为x2+
时原方程可化为x2+ x+
x+ =0,解得x=-
=0,解得x=- 或x=-1(不合题意舍去).
或x=-1(不合题意舍去).故AB=4,BC=6,
∵△AED的面积是△DEM的高相同,
∴△AED的面积是△DEM面积的3倍则AE=3ME,设
ME=x,则AE=3x,设BM=y.
在Rt△AED与Rt△MBA中,∵∠ABM=∠AED=90°,∠AMB=∠DAE,故两三角形相似,
由勾股定理得AB2+BM2=16x2----①,解得BM=
 ,
,即
 =
= ,即
,即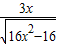 =
= ----②,
----②,整理得x4-4x2+4=0,解得x2=2,x=
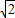 .
.于是BM=
 =
= =4.
=4.当点M离开点B的距离为4时,△AED的面积是△DEM面积的3倍.
点评:此题将动点问题与一元二次方程和矩形的性质相结合,通过相似三角形和同高不等底的三角形的性质,将面积关系转化为线段的性质解答.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
 ;
;

 ;
;
 (2000•金华)如图,要测量河两岸相对的两点A、B间的距离,先从B处出发,与AB成90°角方向,向前走50米到C处立一根标杆,然后方向不变继续朝前走10米到D处,在D处沿垂直于BD的方向再走5米到达E处,使A(目标物),C(标杆)与E在同一直线上,则AB的长为 米.
(2000•金华)如图,要测量河两岸相对的两点A、B间的距离,先从B处出发,与AB成90°角方向,向前走50米到C处立一根标杆,然后方向不变继续朝前走10米到D处,在D处沿垂直于BD的方向再走5米到达E处,使A(目标物),C(标杆)与E在同一直线上,则AB的长为 米.