题目内容
已知:△ABC和△DBE均为等腰直角三角形.如图(1),易证AD=CE且AD⊥CE.
(1)将△DBE绕点B顺时针旋转至图(2)的位置时,线段AD和CE有怎样的关系?
(2)将△DBE绕点B逆时针旋转至图(3)的位置时,线段AD和CE又有怎样的关系?
请直接写出你的猜想,并选择其一加以证明.

(1)将△DBE绕点B顺时针旋转至图(2)的位置时,线段AD和CE有怎样的关系?
(2)将△DBE绕点B逆时针旋转至图(3)的位置时,线段AD和CE又有怎样的关系?
请直接写出你的猜想,并选择其一加以证明.

分析:(1)根据等腰直角三角形的性质可得AB=BC,BD=BE,∠ABC=∠DBE=90°,然后利用“边角边”证明△ABD和△CBE全等,根据全等三角形对应边相等可得AD=CE,全等三角形对应角相等可得∠BAD=∠BCE,延长AD交CE于F,然后求出∠BAD+∠BEC=90°,再求出∠AFE=90°,从而判断出AD⊥CE;
(2)根据等腰直角三角形的性质可得AB=BC,BD=BE,∠ABC=∠DBE=90°,再求出∠ABD=∠CBE,然后利用“边角边”证明△ABD和△CBE全等,根据全等三角形对应边相等可得AD=CE,全等三角形对应角相等可得∠BAD=∠BCE,设AD、CE交点为F,然后求出∠ACF+∠CAF=∠ACB+∠CAB=90°,再求出∠AFC=90°,从而判断出AD⊥CE.
(2)根据等腰直角三角形的性质可得AB=BC,BD=BE,∠ABC=∠DBE=90°,再求出∠ABD=∠CBE,然后利用“边角边”证明△ABD和△CBE全等,根据全等三角形对应边相等可得AD=CE,全等三角形对应角相等可得∠BAD=∠BCE,设AD、CE交点为F,然后求出∠ACF+∠CAF=∠ACB+∠CAB=90°,再求出∠AFC=90°,从而判断出AD⊥CE.
解答: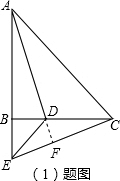 解:(1)AD=CE且AD⊥CE.
解:(1)AD=CE且AD⊥CE.
理由如下:∵△ABC和△DBE均为等腰直角三角形,
∴AB=BC,BD=BE,∠ABC=∠DBE=90°,
在△ABD和△CBE中,
,
∴△ABD≌△CBE(SAS),
∴AD=CE,∠BAD=∠BCE,
延长AD交CE于F,
∵∠BCE+∠BEC=90°,
∴∠BAD+∠BEC=90°,
∴∠AFE=180°-90°=90°,
∴AD⊥CE;
(2)AD=CE且AD⊥CE.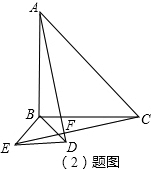
理由如下:∵△ABC和△DBE均为等腰直角三角形,
∴AB=BC,BD=BE,∠ABC=∠DBE=90°,
∴∠ABC+∠CBD=∠DBE+∠CBD,
即∠ABD=∠CBE,
在△ABD和△CBE中,
,
∴△ABD≌△CBE(SAS),
∴AD=CE,∠BAD=∠BCE,
设AD、CE交点为F,
则∠ACF+∠CAF=∠ACB+∠CAB=90°,
∴∠AFC=180°-90°=90°,
∴AD⊥CE.
 解:(1)AD=CE且AD⊥CE.
解:(1)AD=CE且AD⊥CE.理由如下:∵△ABC和△DBE均为等腰直角三角形,
∴AB=BC,BD=BE,∠ABC=∠DBE=90°,
在△ABD和△CBE中,
|
∴△ABD≌△CBE(SAS),
∴AD=CE,∠BAD=∠BCE,
延长AD交CE于F,
∵∠BCE+∠BEC=90°,
∴∠BAD+∠BEC=90°,
∴∠AFE=180°-90°=90°,
∴AD⊥CE;
(2)AD=CE且AD⊥CE.

理由如下:∵△ABC和△DBE均为等腰直角三角形,
∴AB=BC,BD=BE,∠ABC=∠DBE=90°,
∴∠ABC+∠CBD=∠DBE+∠CBD,
即∠ABD=∠CBE,
在△ABD和△CBE中,
|
∴△ABD≌△CBE(SAS),
∴AD=CE,∠BAD=∠BCE,
设AD、CE交点为F,
则∠ACF+∠CAF=∠ACB+∠CAB=90°,
∴∠AFC=180°-90°=90°,
∴AD⊥CE.
点评:本题考查了旋转的性质,主要利用了等腰直角三角形的性质,全等三角形的判定与性质,此类题目,往往利用统一思路根据相同的条件求解,本题确定出三角形全等的条件是解题的关键.

练习册系列答案
相关题目

 已知,△ABC和△CDE都是等边三角形,且点B,C,D在同一条直线上.求证:BE=AD.
已知,△ABC和△CDE都是等边三角形,且点B,C,D在同一条直线上.求证:BE=AD.