题目内容
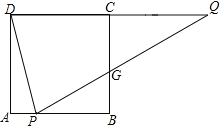
【题目】如图,在边长为2的正方形ABCD中,点P在AB上,点Q在DC的延长线上,连接DP,QP,且∠APD=∠QPD,PQ交BC于点G.
(1)求证:DQ=PQ;
(2)当tan∠APD=![]() 时,求:①CQ的长;②BG的长.
时,求:①CQ的长;②BG的长.
【答案】(1)见解析;(2)①CQ=![]() ;②BG=
;②BG=![]() .
.
【解析】
(1)根据正方形的性质得到AB∥CD,根据平行线的性质得到∠APD=∠QDP.等量代换得到∠QPD=∠QDP,根据等腰三角形的判定定理即可得到结论;
(2)①过Q作QE⊥PD于E,解直角三角形得到AP=1.5,根据勾股定理得到PD=![]() ,DQ=
,DQ=![]() ,于是得到结论;②根据相似三角形的性质列方程即可得到结论.
,于是得到结论;②根据相似三角形的性质列方程即可得到结论.
(1)证明:∵四边形ABDF是正方形,
∴AB∥CD,
∴∠APD=∠QDP.
∵∠APD=∠QPD,
∴∠QPD=∠QDP,
∴DQ=PQ;
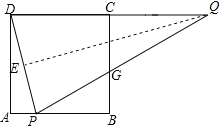
(2)解:①过Q作QE⊥PD于E,
∵四边形ABCD是正方形,
∴∠A=90°,
∵tan∠APD=![]() ,AD=2,
,AD=2,
∴AP=1.5,
∴PD=![]() =
=![]() ,
,
∵DQ=PQ,
∴DE=PE=![]() ,
,
∵∠APD=∠QPD,
∴tan∠APD=![]() =tan∠QPD=
=tan∠QPD=![]() ,
,
∴QE=![]() ,
,
∴DQ=![]() =
=![]() ,
,
∴CQ=DQ-CD=![]() ;
;
②∵AB=2,AP=1.5,
∴PB=![]() ,
,
∵CQ∥PB,
∴△CQG∽△BPG,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴BG=![]() .
.
故答案为:(1)见解析;(2)①CQ=![]() ;②BG=
;②BG=![]() .
.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目