题目内容
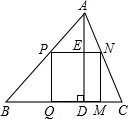
如图，有一块三角形余料ABC，它的边BC=120cm，高AD=80cm，要把它加工成正方形零件PQMN，使正方形的一边QM在BC上，其余两个顶点P、N分别在AB、AC上，则加工成的正方形零件的边长是
- A.48cm
- B.46cm
- C.42cm
- D.40cm
A
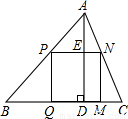
分析：根据正方形边的平行关系，得出对应的相似三角形，即△APM∽△ABC，△BPQ∽△BAD，从而得出边长之比，进而求出正方形的边长；
解答：设正方形零件的边长为a
在正方形PMQN中，PM∥BC，PQ∥AD，
∴△APM∽△ABC，△BPQ∽△BAD
∴
=
，
=
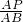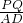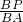
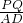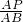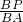∴+=+=1
即：
+
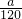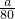=1
解得：a=48
故选A．
点评：本题考查综合考查相似三角形性质的应用以及正方形的有关性质，解题的关键是根据正方形的性质得到相似三角形．
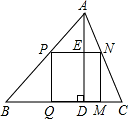
分析：根据正方形边的平行关系，得出对应的相似三角形，即△APM∽△ABC，△BPQ∽△BAD，从而得出边长之比，进而求出正方形的边长；
解答：设正方形零件的边长为a
在正方形PMQN中，PM∥BC，PQ∥AD，
∴△APM∽△ABC，△BPQ∽△BAD
∴
=，=∴
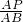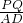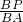
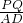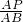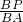+=+=1即：
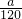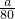+=1解得：a=48
故选A．
点评：本题考查综合考查相似三角形性质的应用以及正方形的有关性质，解题的关键是根据正方形的性质得到相似三角形．
练习册系列答案
阅读快车系列答案
相关题目
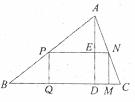
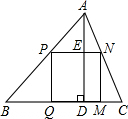如图，有一块三角形余料ABC，它的边BC=120cm，高AD=80cm，要把它加工成正方形零件PQMN，使正方形的一边QM在BC上，其余两个顶点P、N分别在AB、AC上，则加工成的正方形零件的边长是（ ）
