题目内容
(2013年四川资阳3分)已知直线上有n(n≥2的正整数)个点,每相邻两点间距离为1,从左边第1个点起跳,且同时满足以下三个条件:
①每次跳跃均尽可能最大;
②跳n次后必须回到第1个点;
③这n次跳跃将每个点全部到达,
设跳过的所有路程之和为Sn,则S25= .
①每次跳跃均尽可能最大;
②跳n次后必须回到第1个点;
③这n次跳跃将每个点全部到达,
设跳过的所有路程之和为Sn,则S25= .
312。
设这n个点从左向右依次编号为A1,A2,A3,…,An.
根据题意,n次跳跃的过程可以列表如下:
发现规律如下:
当n为偶数时,跳跃的路程为: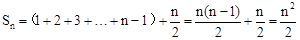 ;
;
当n为奇数时,跳跃的路程为: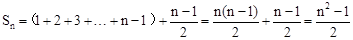 。
。
因此,当n=25时,跳跃的路程为: 。
。
根据题意,n次跳跃的过程可以列表如下:
发现规律如下:
| 第n次跳跃 | 起点 | 终点 | 路程 | |
| 1 | A1 | An | n-1 | |
| 2 | An | A2 | n-2 | |
| 3 | A2 | An-1 | n-3 | |
| … | … | … | … | |
| n-1 | n为偶数 | 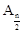 | 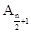 | 1 |
| n为奇数 | 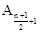 | 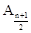 | 1 | |
| n | n为偶数 | 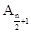 | A1 | 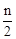 |
| n为奇数 | 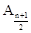 | A1 | 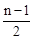 | |
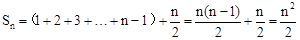 ;
;当n为奇数时,跳跃的路程为:
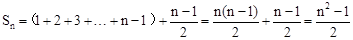 。
。因此,当n=25时,跳跃的路程为:
 。
。
练习册系列答案
相关题目
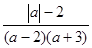 的值为0,则a= .
的值为0,则a= .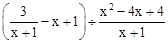 ,然后从﹣1≤x≤2中选一个合适的整数作为x的值代入求值.
,然后从﹣1≤x≤2中选一个合适的整数作为x的值代入求值. .
. 的值为零,则x的值为
的值为零,则x的值为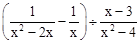 ,其中x=4.
,其中x=4. 的结果是
的结果是 ;
; .
.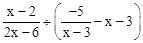 ,其中
,其中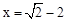 .
.