题目内容
已知平面区域上,坐标x,y满足|x|+|y|≤1(1)画出满足条件的区域L0,并求出面积S;
(2)对区域L0作一个内切圆M1,然后在M1内作一个内接与此圆与L0相同形状的图形L1,在L1内继续作圆M2,…经过无数次后,求所有圆的面积的和.
(提示公式:(1)a+(a+d)+(a+2d)+…(a+nd)=
| (a+(a+nd))*n |
| 2 |
| a-aqn*q |
| 1-q |
分析:(1)根据绝对值的性质去掉绝对值号,作出|x|+|y|≤1的线性规划区域即可得到区域L0,然后根据正方形的面积等于对角线乘积的一半进行求解即可;
(2)求出M1、M2的面积,然后根据求解规律,后一个圆得到面积等于前一个圆的面积的
,然后列式,再根据等比数列的求和公式求解即可.
(2)求出M1、M2的面积,然后根据求解规律,后一个圆得到面积等于前一个圆的面积的
| 1 |
| 4 |
解答: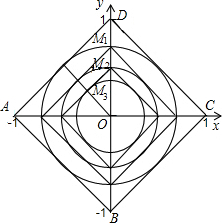 解:(1)如图,|x|+|y|≤1可化为,
解:(1)如图,|x|+|y|≤1可化为,
x+y≤1,x-y≤,-x+y≤1,-x-y≤1,
∴四边形ABCD就是满足条件的区域L0是正方形,
S=
×AC×BD=
×(1+1)×(1+1)=2;
(2)如图,∵A0=1,
∴⊙M1的半径为:1×sin45°=
,
∴内切圆M1的面积是:π(
)2=
π,
同理可得:⊙M2的半径为:
×sin45°=(
)2,
∴内切圆M2的面积是:π[(
)2]2=
π×
=π(
)2,
⊙M3的半径为:(
)2×sin45°=(
)3,
内切圆M3的面积是:π[(
)3]2=
π×(
)2=π(
)3,
…
以此类推,经过n次后,⊙Mn的面积为π(
)n,
∴所有圆的面积的和=
π+π(
)2+π(
)3+…+π(
)n=
=π[1-(
)n].
故答案为:(1)2,(2)π[1-(
)n].
 解:(1)如图,|x|+|y|≤1可化为,
解:(1)如图,|x|+|y|≤1可化为,x+y≤1,x-y≤,-x+y≤1,-x-y≤1,
∴四边形ABCD就是满足条件的区域L0是正方形,
S=
| 1 |
| 2 |
| 1 |
| 2 |
(2)如图,∵A0=1,
∴⊙M1的半径为:1×sin45°=
| ||
| 2 |
∴内切圆M1的面积是:π(
| ||
| 2 |
| 1 |
| 2 |
同理可得:⊙M2的半径为:
| ||
| 2 |
| ||
| 2 |
∴内切圆M2的面积是:π[(
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
⊙M3的半径为:(
| ||
| 2 |
| ||
| 2 |
内切圆M3的面积是:π[(
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
…
以此类推,经过n次后,⊙Mn的面积为π(
| 1 |
| 2 |
∴所有圆的面积的和=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||||
1-
|
| 1 |
| 2 |
故答案为:(1)2,(2)π[1-(
| 1 |
| 2 |
点评:本题综合考查了一次函数与圆的面积的问题,作出图形,求出后一个圆的半径等于前一个圆的半径的
倍是解题的关键.
| ||
| 2 |

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
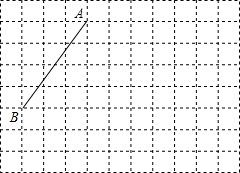 如图:线段AB的端点在边长为1的小正方形网格的格点上,现将线段AB绕点A按逆时针方向旋转90°得到线段AC.
如图:线段AB的端点在边长为1的小正方形网格的格点上,现将线段AB绕点A按逆时针方向旋转90°得到线段AC.
 )
)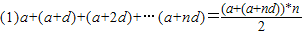
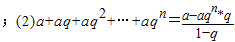 )
)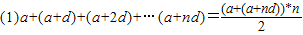
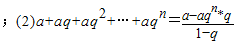 )
)