题目内容
AE、CF是锐角三角形ABC的两条高，若AE：CF=3：2，则sinA：sinC等于分析：运用锐角三角函数的定义解答．
解答：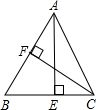
解：如图，由锐角三角函数的定义可知，
∵sinA=
，sinC=
，
∴sinA：sinC=
：
=FC：AE=2：3．
故答案为：2：3．
解：如图，由锐角三角函数的定义可知，∵sinA=
| FC |
| AC |
| AE |
| AC |
∴sinA：sinC=
| FC |
| AC |
| AE |
| AC |
故答案为：2：3．
点评：本题考查了锐角三角函数的定义，比较简单．
练习册系列答案
相关题目
AE、CF是锐角三角形ABC的两条高，如果AE：CF=3：2，则sinA：sinC等于（ ）
| A、3：2 | B、2：3 | C、9：4 | D、4：9 |