题目内容
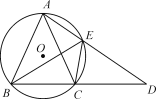
【题目】如图,已知⊙O是△ABC的外接圆,AD是⊙O的直径,且BD=BC,延长AD到E,且有∠EBD=∠CAB.
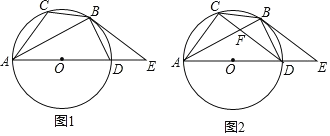
(1)如图1,若BD=![]() ,AC=6
,AC=6
A.求证:BE为圆O的切线
B.求DE的长
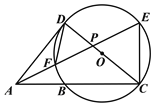
(2)如图2,连结CD交AB于点F,若BD=![]() ,CF=3,求圆O的半径.
,CF=3,求圆O的半径.
【答案】(1)A.见解析;B.![]() ;(2)5
;(2)5
【解析】
(1)A.连接OB,由条件可求得∠EBD=∠ABO,再利用圆周角定理可求得∠EBD+∠OBD=90°,可证明BE是⊙O的切线;
B.利用圆内接四边形的性质可求得∠BDE=∠ACB,可证明△ACB∽△BDE,利用相似三角形的性质可求得DE的长;
(2)延长DB、AC交于点H,可证得△ABD≌△ABH,可求得HB,再利用△DCH∽△DBF,可求得DF的长,设⊙O的半径为r,则AD=AH=2r,在Rt△DCH中可求得CH=4,在Rt△ADC中,AD=2r,CD=8,AC=2r-4,由勾股定理可得到关于r的方程,可求得圆的半径.
(1) A.如图1,连接OB,
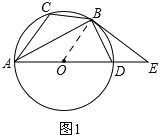
∵BD=BC,
∴∠CAB=∠BAD,
∵∠EBD=∠CAB,
∴∠BAD=∠EBD,
∵AD是⊙O的直径,
∴∠ABD=90°,OA=BO,
∴∠BAD=∠ABO,
∴∠EBD=∠ABO,
∴∠OBE=∠EBD+∠OBD=∠ABD+∠OBD=∠ABD=90°,
∵点B在⊙O上,
∴BE是⊙O的切线;
B.∵四边形ACBD是圆的内接四边形,
∴∠ACB=∠BDE,且∠EBD=∠CAB,
∴△ACB∽△BDE,
∴![]() =
=![]() ,即
,即![]() ,
,
解得DE=![]() ;
;
(2)如图2,延长DB、AC交于点H,
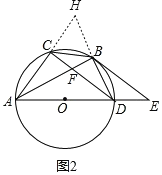
∵AD为⊙O的直径,
∴∠ABD=∠ABH=90°,
∵BD=BC,
∴∠DAB=∠HAB,
在△ABD和△ABH中
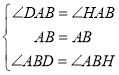
∴△ABD≌△ABH(ASA),
∴BD=HB=![]() ,
,
∵∠DCH=∠FBD=90°,
∴△DCH∽△DBF,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,解得DF=5,
,解得DF=5,
设⊙O的半径为r,则AD=AH=2r,
在Rt△DCH中,CH=![]() =
=![]() =4,
=4,
∴AC=2r4,
在Rt△ACD中,由勾股定理可得AD2=AC2+CD2,
∴(2r)2=(2r4)2+82,解得r=5,
即⊙O的半径为5.