��Ŀ����
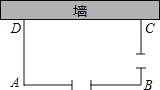
����Ŀ����ͼ������һ�泤Ϊ34��ǽ������դ��Χ��һ���������г�����ABCD����AB��BC�߸���һ��2����С�ţ�������դ���������ABCD�ı�AD��Ϊx�ף�AB��Ϊy�ף����ε����ΪSƽ���ף���x��y��
��1����������դ���ij�Ϊ40�ף�д��y��x�ĺ�����ϵʽ��������Ա���x��ȡֵ��Χ��
��2���ڣ�1���������£���S��x�ĺ�����ϵʽ�����������Χ����ʹ���γ��ص����Ϊ192ƽ���ף�
��3���ڣ�2���������£���ֱ��д�������γ��ص��������192ƽ����ʱx��ȡֵ��Χ��
���𰸡���1��y����2x+44��5��x��![]() ������2��S����2x2+44x��AD��Ϊ6��AB��Ϊ32�ף���ʹ���γ��ص����Ϊ192ƽ���ף���3����6��x��32ʱ�����γ��ص��������192ƽ���ף�
������2��S����2x2+44x��AD��Ϊ6��AB��Ϊ32�ף���ʹ���γ��ص����Ϊ192ƽ���ף���3����6��x��32ʱ�����γ��ص��������192ƽ���ף�
��������
��1���������⣬��֪AD+BC+AB��40������AD��BC��������д��y����x�ĺ�����ϵʽ���Ա�����ȡֵ��Χ��
��2���ɣ�1����y��x�ĺ�����ϵʽ���ɵ�S��x�ĺ�����ϵʽ����S��192�����xֵ�����������ʵ����������ȡ�
��3���ɣ�2���еĺ�����ϵʽ�����κ��������ʣ��ɵô𰸣�
�⣺��1��������ã�y��2+x+x��2��40
��y����2x+44
��x��y
��x����2x+44
��x��![]()
�߳�Ϊ34��ǽ
�ੁ2x+44��34
��x��5
��5��x��![]() ��
��
��2��S��xy
��x����2x+44��
����2x2+44x
��S��x�ĺ�����ϵʽΪ��S����2x2+44x
��S��192ʱ����
��2x2+44x��192
��ã�x1��6��x2��16
��x2��16��![]()
��x2��16���������⣬��ȥ��
��y����2��6+44��32
��AD��Ϊ6��AB��Ϊ32�ף���ʹ���γ��ص����Ϊ192ƽ���ף�
��3���ɣ�2����֪��S����x�Ŀ������µĶ��κ���
�൱6��x��32ʱ�����γ��ص��������192ƽ���ף�