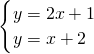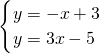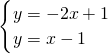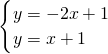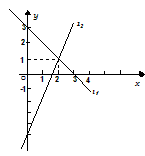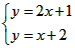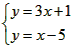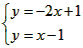题目内容
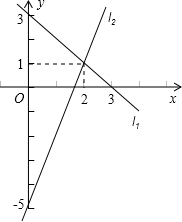 如图,两条直线l1和l2的交点坐标可以看作下列方程组中的解( )
如图,两条直线l1和l2的交点坐标可以看作下列方程组中的解( )A、
| |||||
B、
| |||||
C、
| |||||
D、
|
分析:因为函数图象交点坐标为两函数解析式组成的方程组的解.因此本题应该先用待定系数法求出两条直线的解析式,联立两直线解析式所组成的方程组即为所求的方程组.
解答:解:由图知:直线l1的图象经过点(2,1),(0,3);因此直线l1的解析式是:y=-x+3;
同理可求得直线l2的解析式为:y=3x-5;
所以两条直线l1和l2的交点坐标可以看作方程组
的解.
故选B.
同理可求得直线l2的解析式为:y=3x-5;
所以两条直线l1和l2的交点坐标可以看作方程组
|
故选B.
点评:在同一平面直角坐标系中,两个一次函数图象的交点坐标就是相应的二元一次方程组的解.反过来,以二元一次方程组的解为坐标的点,一定是相应的两个一次函数的图象的交点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,平面中两条直线l1和l2相交于点O,对于平面上任意一点M,若p、q分别是M到直线l1和l2的距离,则称有序非负实数对(p,q)是点M的“距离坐标”.根据上述定义,有以下几个结论:
如图,平面中两条直线l1和l2相交于点O,对于平面上任意一点M,若p、q分别是M到直线l1和l2的距离,则称有序非负实数对(p,q)是点M的“距离坐标”.根据上述定义,有以下几个结论: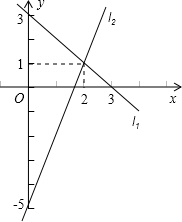 如图,两条直线l1和l2的交点坐标可以看作下列方程组中的解
如图,两条直线l1和l2的交点坐标可以看作下列方程组中的解