Question

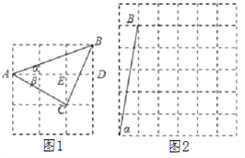
【题目】(1)如图1，如果ɑ，β都为锐角，且tanɑ=，tanβ=，则ɑ+β=___________；

(2)如果ɑ，β都为锐角，当tanɑ=5，tanβ=时，在图2的正方形网格中，利用已作出的锐角ɑ，画出∠MON，使得∠MON=ɑ-β.此时ɑ-β=__________度.

Answer 1

【答案】 45° 45°

【解析】（1））如图1中，只要证明△AMC≌△CNB，即可证明△ACB是等腰直角三角形．

（2）如图2中，∠MOE=α，∠NOH=β，∠MON=α-β，只要证明△MFN≌△NHO即可解决问题．

（1）①如图1中，

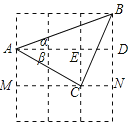
在△AMC和△CNB中，

，

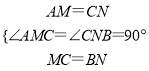∴△AMC≌△CNB，

∴AC=BC，∠ACM=∠CBN，

∵∠BCN+∠CBN=90°，

∴∠ACM+∠BCN=90°，

∴∠ACB=90°，

∴∠CAB=∠CBA=45°，

∴α+β=45°．

（2）如图，∠MOE=α，∠NOH=β，∠MON=α-β．

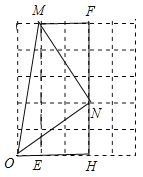
在△MFN和△NHO中，

，

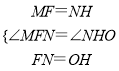∴△MFN≌△NHO，

∴MN=NO，∠MNF=∠NOH，

∵∠NOH+∠ONH=90°，

∴∠ONH+∠MNF=90°，

∴∠MNO=90°，

∴∠NOM=∠NMO=45°，

∴α-β=45°．