题目内容
(1)如图(1),可以求出阴影部分的面积是______.(写成两数平方差的形式)
(2)如图(2),若把阴影部分裁剪下来,重新拼成一个长方形,则它的面积是______.(写成多项式乘法的形式)
(3)比较图(1)、(2)中阴影部分的面积,可以得到乘法公式______.
(4)运用你所得到的公式,完成下列各题:
①分解因式:4x2-16
②计算:(2m+n-p)(2m-n+p)
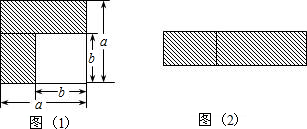
解:(1)图1中阴影部分的面积=边长为a的正方形的面积-边长为b的正方形面积=a2-b2;
(2)图2中的长方形面积=(a-b)(a+b);
(3)∵图2中的长方形面积=图1中阴影部分的面积,
∴(a-b)(a+b)=a2-b2;
(4)①原式=4(x2-22)
=4(x+2)(x-2);
②原式=[2m+(n-p)][2m-(n-p)]
=(2m)2-(n-p)2
=4m2-(n2+p2-2np)
=4m2-n2-p2+2np.
故答案为a2-b2;(a-b)(a+b);(a+b)(a-b)=a2-b2.
分析:(1)图1中阴影部分的面积等于边长为a的正方形的面积与边长为b的正方形面积之差;
(2)图2中的长方形的宽为a-b,长为a+b,然后利用矩形面积公式求解;
(3)由于图2中的长方形由图1中阴影部分拼成,则图2中的长方形面积=图1中阴影部分的面积,所以(a-b)(a+b)=a2-b2;
(4)①先提4得到两个数的平方差,然后运用平方差公式分解得到4(x+2)(x-2);
②先变形得到[2m+(n-p)][2m-(n-p)],符号平方差公式,然后利用平方差公式展开得到(2m)2-(n-p)2,再利用完全平方公式展开即可.
点评:本题考查了平方差公式的几何背景:运用面积法证明平方差公式(a+b)(a-b)=a2-b2.
(2)图2中的长方形面积=(a-b)(a+b);
(3)∵图2中的长方形面积=图1中阴影部分的面积,
∴(a-b)(a+b)=a2-b2;
(4)①原式=4(x2-22)
=4(x+2)(x-2);
②原式=[2m+(n-p)][2m-(n-p)]
=(2m)2-(n-p)2
=4m2-(n2+p2-2np)
=4m2-n2-p2+2np.
故答案为a2-b2;(a-b)(a+b);(a+b)(a-b)=a2-b2.
分析:(1)图1中阴影部分的面积等于边长为a的正方形的面积与边长为b的正方形面积之差;
(2)图2中的长方形的宽为a-b,长为a+b,然后利用矩形面积公式求解;
(3)由于图2中的长方形由图1中阴影部分拼成,则图2中的长方形面积=图1中阴影部分的面积,所以(a-b)(a+b)=a2-b2;
(4)①先提4得到两个数的平方差,然后运用平方差公式分解得到4(x+2)(x-2);
②先变形得到[2m+(n-p)][2m-(n-p)],符号平方差公式,然后利用平方差公式展开得到(2m)2-(n-p)2,再利用完全平方公式展开即可.
点评:本题考查了平方差公式的几何背景:运用面积法证明平方差公式(a+b)(a-b)=a2-b2.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目



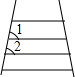 如图,∠1和∠2可看成是一对( )
如图,∠1和∠2可看成是一对( )