题目内容
【题目】如图,点E在以AB为直径的⊙O上,点C是 ![]() 的中点,过点C作CD垂直于AE,交AE的延长线于点D,连接BE交AC于点F.
的中点,过点C作CD垂直于AE,交AE的延长线于点D,连接BE交AC于点F. 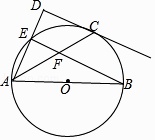
(1)求证:CD是⊙O的切线;
(2)若cos∠CAD= ![]() ,BF=15,求AC的长.
,BF=15,求AC的长.
【答案】
(1)证明:连接OC,如图1所示.
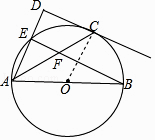
∵点C是 ![]() 的中点,
的中点,
∴ ![]() =
= ![]() ,
,
∴OC⊥BE.
∵AB是⊙O的直径,
∴AD⊥BE,
∴AD∥OC.
∵AD⊥CD,
∴OC⊥CD,
∴CD是⊙O的切线.
(2)解:过点O作OM⊥AC于点M,如图2所示.
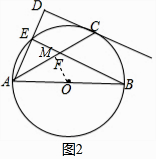
∵点C是 ![]() 的中点,
的中点,
∴ ![]() =
= ![]() ,∠BAC=∠CAE,
,∠BAC=∠CAE,
∴ ![]() =
= ![]() .
.
∵cos∠CAD= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴AB= ![]() BF=20.
BF=20.
在Rt△AOM中,∠AMO=90°,AO= ![]() AB=10,cos∠OAM=cos∠CAD=
AB=10,cos∠OAM=cos∠CAD= ![]() ,
,
∴AM=AOcos∠OAM=8,
∴AC=2AM=16.
【解析】(1)连接OC,由点C是 ![]() 的中点利用垂径定理可得出OC⊥BE,由AB是⊙O的直径可得出AD⊥BE,进而可得出AD∥OC,再根据AD⊥CD可得出OC⊥CD,由此即可证出CD是⊙O的切线.(2)过点O作OM⊥AC于点M,由点C是
的中点利用垂径定理可得出OC⊥BE,由AB是⊙O的直径可得出AD⊥BE,进而可得出AD∥OC,再根据AD⊥CD可得出OC⊥CD,由此即可证出CD是⊙O的切线.(2)过点O作OM⊥AC于点M,由点C是 ![]() 的中点利用圆周角定理可得出∠BAC=∠CAE,根据角平分线的定理结合cos∠CAD=
的中点利用圆周角定理可得出∠BAC=∠CAE,根据角平分线的定理结合cos∠CAD= ![]() 可求出AB的长度,在Rt△AOM中,通过解直角三角形可求出AM的长度,再根据垂径定理即可得出AC的长度.
可求出AB的长度,在Rt△AOM中,通过解直角三角形可求出AM的长度,再根据垂径定理即可得出AC的长度.
【考点精析】本题主要考查了解直角三角形的相关知识点,需要掌握解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)才能正确解答此题.

练习册系列答案
相关题目