题目内容
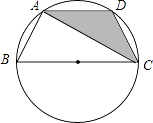
【题目】如图1，△ABC是等腰直角三角形，∠BAC=90°，AB=AC，四边形ADEF是正方形，点B．C分别在边AD、AF上，此时BD=CF，BD⊥CF成立．
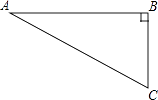
（1）当△ABC绕点A逆时针旋转θ（0°＜θ＜90°）时，如图2，BD=CF成立吗？若成立，请证明，若不成立，请说明理由．
（2）当△ABC绕点A逆时针旋转45°时，如图3，延长BD交CF于点H．
①探究BD与CF之间的位置关系，并说明理由；
②当AB= 
，AD= 
+1时，求线段DH的长．
【答案】
（1）
解：如图2中，BD=CF成立．
理由：由旋转得：AC=AB，∠CAF=∠BAD=θ；AF=AD，
在△ABD和△ACF中， 
，
∴△ABD≌△ACF，
∴BD=CF
（2）
①证明：如图3中，
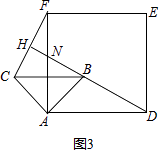
由（1）得，△ABD≌△ACF，
∴∠HFN=∠ADN，
∵∠HNF=∠AND，∠AND+∠AND=90°
∴∠HFN+∠HNF=90°
∴∠NHF=90°，
∴HD⊥HF，即BD⊥CF．
②如图4中，连接DF，延长AB，与DF交于点M．
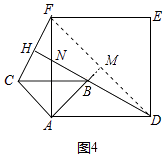
∵四边形ADEF是正方形，
∴∠MDA=45°，
∵∠MAD=45°
∴∠MAD=∠MDA，∠AMD=90°，
∴AM=DM，
∵AD= 
+1，
在△MAD中，AM2+DM2=AD2，
∴AM=DM= 
，
∴MB=AM﹣AB= ﹣ 
= 
，
在Rt△BMD中，BM2+DM2=BD2，
∴BD= 
=2．
在Rt△ADF中，AD= +1，
∴DF= AD= 
+ ，
由②知，HD⊥HF，
∴∠DHF=∠DMB=90°，
∵∠BDM=∠FDH，
∴△BDM∽△FDH，
∴ 
，
∴DH= 
= 
=2+
【解析】（1）结论：BD=CF．只要证明△ABD≌△ACF即可．（2）①在利用“8字型”证明∠FHN=∠DAN=90°，即可解决问题．②如图4中，连接DF，延长AB，与DF交于点M．在Rt△ADM中，求出BM、DM，再利用勾股定理即可解决问题．
【考点精析】掌握勾股定理的概念是解答本题的根本，需要知道直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2．
