Question

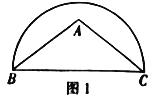
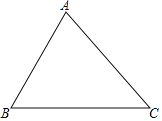
【题目】如图，已知△ABC.（1）请用圆规和直尺作出⊙P，使圆心P到AB边和BC边的距离相等，且⊙P经过A，B两点（保留作图痕迹，不写作法和证明）；

（2）若∠B=60°，AB=6，求⊙P的半径．

Answer 1

【答案】（1）见解析；（2）⊙P的半径为2．

【解析】

（1）先作∠ABC的平分线BD，再作AB的垂直平分线交OD于P，交AB于H，然后以P点为圆心，PB为半径作圆即可；

（2）先利用角平分线得到∠ABP=30°，再根据PH垂直平分AB得到BH=3，然后根据含30度的直角三角形三边的关系计算PB即可．

解：（1）如图，⊙P为所作；

（2）∵点P到AB边和BC边的距离相等，

∴OP平分∠ABC，

∴∠ABP=∠ABC=×60°=30°，

∵PH垂直平分AB，

∴BH=AB=3，

在Rt△PBH中，PH=BH=，

∴PB=2PH=2，

即⊙P的半径为2．