题目内容
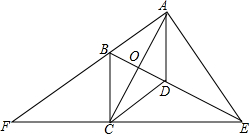 (2013•宜昌模拟)菱形ABCD中,∠BAD是锐角,AC,BD相交于点O,E是BD的延长线上一动点(不与点D重合),连接EC并延长和AB的延长线交于点F,连接AE.
(2013•宜昌模拟)菱形ABCD中,∠BAD是锐角,AC,BD相交于点O,E是BD的延长线上一动点(不与点D重合),连接EC并延长和AB的延长线交于点F,连接AE.(1)比较∠F和∠ABD的大小,并说明理由;
(2)当△BFC有一个内角是直角时,求证:△BFC∽△EFA;
(3)当△BFC与△EFA相似(两三角形的公共角为对应角),且AC=12,DE=5时,求△BFC与△EFA的相似比.
分析:(1)根据三角形外角的性质可作出判断;
(2)推出这个直角为∠BCF,然后证明△△ABE≌△CBE,得出∠FCB=∠FAE=90°,即可证明结论.
(3)根据(2)可得∠BAE=∠BCF=∠BCE=90°,∠FBC=∠AEF,证明△OAD∽△OEA,得出AO2=OD×OE,设OD=x,解出x的值,继而可得出相似比.
(2)推出这个直角为∠BCF,然后证明△△ABE≌△CBE,得出∠FCB=∠FAE=90°,即可证明结论.
(3)根据(2)可得∠BAE=∠BCF=∠BCE=90°,∠FBC=∠AEF,证明△OAD∽△OEA,得出AO2=OD×OE,设OD=x,解出x的值,继而可得出相似比.
解答:解:(1)∵∠ABD为△BFE的一个外角,
∴∠ABD>∠F;
(2)∵四边形ABCD是菱形,
∴BC∥AD,∠ABD=
∠ABC,
∴∠BAD=∠FBC,∠BAD+∠ABC=180°
又∵∠BAD为锐角,
∴∠FBC为锐角,∠ABC为钝角,
∴∠ABD为锐角,
由(1)得:∠F也为锐角,
又∵△BFC有一个角是直角,
∴∠BCF为直角,
∵在△ABE和△CBE中,
∴△ABE≌△CBE,
∴∠BAE=∠BCE=90°,
∴∠FCB=∠FAE=90°,
∴△BFC∽△EFA.
(3)当△BFC与△EFA相似(两三角形的公共角为对应角)时
∵∠BCE为△BFC的外角,
∴∠BCE>∠FBC,∠BCE>∠F,
∴∠BAE=∠BCF=∠BCE=90°,∠FBC=∠AEF,
∴∠OAD=∠OEA
∴△OAD∽△OEA,
∴AO2=OD×OE,
设OD=x,列方程得:36=x(x+5),
解得:x=4,
∴BC:AE=AD:AE=AO:OE=2:3.
∴∠ABD>∠F;
(2)∵四边形ABCD是菱形,
∴BC∥AD,∠ABD=
| 1 |
| 2 |
∴∠BAD=∠FBC,∠BAD+∠ABC=180°
又∵∠BAD为锐角,
∴∠FBC为锐角,∠ABC为钝角,
∴∠ABD为锐角,
由(1)得:∠F也为锐角,
又∵△BFC有一个角是直角,
∴∠BCF为直角,
∵在△ABE和△CBE中,
|
∴△ABE≌△CBE,
∴∠BAE=∠BCE=90°,
∴∠FCB=∠FAE=90°,
∴△BFC∽△EFA.
(3)当△BFC与△EFA相似(两三角形的公共角为对应角)时

∵∠BCE为△BFC的外角,
∴∠BCE>∠FBC,∠BCE>∠F,
∴∠BAE=∠BCF=∠BCE=90°,∠FBC=∠AEF,
∴∠OAD=∠OEA
∴△OAD∽△OEA,
∴AO2=OD×OE,
设OD=x,列方程得:36=x(x+5),
解得:x=4,
∴BC:AE=AD:AE=AO:OE=2:3.
点评:本题考查了相似三角形的判定与性质,解答本题的关键一步在于得出若△BFC与△EFA相似,则∠BCF=∠BAE=90°,有一定难度.

练习册系列答案
相关题目
 (2013•宜昌模拟)已知实数a,b在数轴上的位置如图所示,下列式子的值为正数的是( )
(2013•宜昌模拟)已知实数a,b在数轴上的位置如图所示,下列式子的值为正数的是( )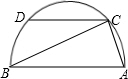 (2013•宜昌模拟)如图,AB是半圆的直径,弦CD∥AB,∠A=65°,∠BCD的度数是( )
(2013•宜昌模拟)如图,AB是半圆的直径,弦CD∥AB,∠A=65°,∠BCD的度数是( )