题目内容
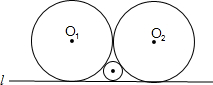 如图,半径为4的两等圆⊙O1、⊙O2都相切,则直线l与⊙O1、⊙O2都相切,则直线l与⊙O1、⊙O2围成的阴影部分中,存在的最大圆的半径等于( )
如图,半径为4的两等圆⊙O1、⊙O2都相切,则直线l与⊙O1、⊙O2都相切,则直线l与⊙O1、⊙O2围成的阴影部分中,存在的最大圆的半径等于( )A、
| ||
B、
| ||
C、
| ||
| D、1 |
分析:根据题意可得最大的圆要与l、⊙O1、⊙O2都相切,设这个最大圆的圆心、半径分别为A,r,连接O1O2,AO1AO2,再连接两等圆的公切点B与A,根据勾股定理可求得答案.
解答: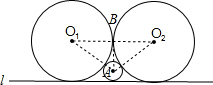 解:设这个最大圆的圆心、半径分别为A,r,
解:设这个最大圆的圆心、半径分别为A,r,
连接O1O2,AO1AO2,再连接两等圆的公切点B与A,
∴AB⊥O1O2,
在Rt△AO1B中,(4+r)2-(4-r)2=16,
解得r=1.
故选D.
 解:设这个最大圆的圆心、半径分别为A,r,
解:设这个最大圆的圆心、半径分别为A,r,连接O1O2,AO1AO2,再连接两等圆的公切点B与A,
∴AB⊥O1O2,
在Rt△AO1B中,(4+r)2-(4-r)2=16,
解得r=1.
故选D.
点评:本题考查了相切两圆的性质以及勾股定理,注:两圆的连心线必过切点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
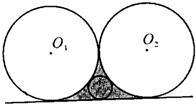 12、如图,半径为4的两等圆相外切,它们的一条外公切线与两圆围成的阴影部分中,存在的最大圆的半径等于
12、如图,半径为4的两等圆相外切,它们的一条外公切线与两圆围成的阴影部分中,存在的最大圆的半径等于




