题目内容
如图，在四边形ABCD中，E、F、G、H分别是AB、BC、CD、AD的中点，要使四边形EFGH是正方形，对角线AC、BD应满足的条件是______．
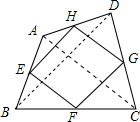
添加的条件应为：AC=BD且AC⊥BD．
理由：∵E，F，G，H分别是边AB、BC、CD、DA的中点，
∴在△ADC中，HG为△ADC的中位线，所以HG∥AC且HG=
AC；同理EF∥AC且EF=
AC，同理可得EH=
BD，
则HG∥EF且HG=EF，
∴四边形EFGH为平行四边形，又AC=BD，所以EF=EH，
∴四边形EFGH为菱形，
∵AC⊥BD，EF∥AC，
∴EF⊥BD，
∵EH∥BD，
∴EF⊥EH，
∴∠FEH=90°，
∴菱形EFGH是正方形．
故答案为：AC=BD且AC⊥BD．
理由：∵E，F，G，H分别是边AB、BC、CD、DA的中点，
∴在△ADC中，HG为△ADC的中位线，所以HG∥AC且HG=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
则HG∥EF且HG=EF，
∴四边形EFGH为平行四边形，又AC=BD，所以EF=EH，
∴四边形EFGH为菱形，
∵AC⊥BD，EF∥AC，
∴EF⊥BD，
∵EH∥BD，
∴EF⊥EH，
∴∠FEH=90°，
∴菱形EFGH是正方形．
故答案为：AC=BD且AC⊥BD．
练习册系列答案
字词句段篇系列答案
相关题目
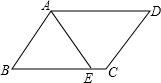
Q从点C出发，沿CB向点B运动，P、Q的运动速度均为1cm/s，两点中有一点到达目的地时，另一点也停止运动，
