题目内容
已知p、q满足等式|p+2|+(q-4)2=0,分解因式:(x2+y2)-(pxy+q)=
(x+y+2)(x+y-2)
(x+y+2)(x+y-2)
.分析:首先根据绝对值的性质以及偶次方的性质得出p,q的值,进而得出利用分组分解法因式分解.
解答:解:∵|p+2|+(q-4)2=0,
∴p=-2,q=4,
∴(x2+y2)-(pxy+q)
=(x2+y2)-(-2xy+4)
=x2+y2+2xy-4,
=(x+y)2-4,
=(x+y+2)(x+y-2).
故答案为:(x+y+2)(x+y-2).
∴p=-2,q=4,
∴(x2+y2)-(pxy+q)
=(x2+y2)-(-2xy+4)
=x2+y2+2xy-4,
=(x+y)2-4,
=(x+y+2)(x+y-2).
故答案为:(x+y+2)(x+y-2).
点评:此题主要考查了分组分解法以及公式法分解因式,熟练掌握公式法分解因式是解题关键.

练习册系列答案
相关题目
已知x,y满足等式2x+x2+x2y2+2=2xy,那么x+y的值为( )
| A、-1 | B、-2 | C、2 | D、1 |
已知a、b满足等式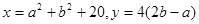 ,则x、y的大小关系是( )
,则x、y的大小关系是( )
| A.x≤y | B.x≥y | C.x<y | D.x>y |
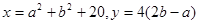 ,则x、y的大小关系是( )
,则x、y的大小关系是( )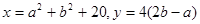 ,则x、y的大小关系是( )
,则x、y的大小关系是( )