题目内容
【题目】如图,平面直角坐标系xOy中,点A在第一象限,B(2,0),∠AOB=60°,∠ABO=90°.在x轴上取一点P(m,0),过点P作直线l垂直于直线OA,将OB关于直线l的对称图形记为O′B′,当O′B′和过A点且平行于x轴的直线有交点时,m的取值范围为( )

A.m≥4B.m≤6C.4<m<6D.4≤m≤6
【答案】D
【解析】
根据题意可以作出合适的辅助线,然后根据题意,利用分类讨论的方法可以计算出m的两个极值,从而可以得到m的取值范围.
解:如图所示,
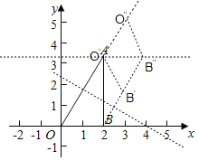
当直线l垂直平分OA时,O′B′和过A点且平行于x轴的直线有交点,
∵点A在第一象限,B(2,0),∠AOB=60°,∠ABO=90°,
∴∠BAO=30°,OB=2,
∴OA=4,
∵直线l垂直平分OA,点P(m,0)是直线l与x轴的交点,
∴OP=4,
∴当m=4;
作BB″∥OA,交过点A且平行于x轴的直线与B″,
当直线l垂直平分BB″和过A点且平行于x轴的直线有交点,
∵四边形OBB″O′是平行四边形,
∴此时点P与x轴交点坐标为(6,0),
由图可知,当OB关于直线l的对称图形为O′B′到O″B″的过程中,点P符合题目中的要求,
∴m的取值范围是4≤m≤6,
故选:D.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


