题目内容
【题目】
(1)解题探究
已知三角形ABC,探究∠A+∠B+∠C等于多少度?(提示:过一点作平行线)

(2)发现规律
如图①,三角形ABC中,点D在BC的延长线上,试说明∠A+∠B与∠1的关系?

(3)运用规律
利用以上规律,快速探究以下各图:



当AB∥CD时,∠A,∠C,∠P的关系式为(直接填空,不要证明过程):
∠C = ,∠C = ,∠C =
【答案】(1)180°;(2)∠A+∠B=∠1;(3)∠A+∠P,∠A-∠P,∠P+180°-∠A.
【解析】试题分析:(1)延长BC到D,过点C作CE∥BA,根据两直线平行,同位角相等可得∠B=∠1,两直线平行,内错角相等可得∠A=∠2,再根据平角的定义列式整理即可得证;
(2)根据平行线的性质即可得到结论;
(3)根据平行线的性质和三角形的外角的性质即可得到结论.
试题解析:(1)如图⑤,延长BC到D,过点C作CE∥BA,
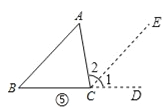
∵BA∥CE,
∴∠B=∠1(两直线平行,同位角相等),
∠A=∠2(两直线平行,内错角相等),
又∵∠BCD=∠BCA+∠2+∠1=180°(平角的定义),
∴∠A+∠B+∠ACB=180°(等量代换);
(2)如图①过C作CE∥AB,
∴∠2=∠A,∠3=∠B,
∴∠ACD=∠1+∠2=∠A+∠B,
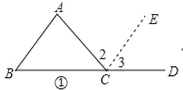
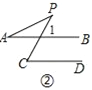
(3)如图②,∵AB∥CD,
∴∠1=∠C,
∵∠1=∠A+∠P,
∴∠C=∠A+∠P;
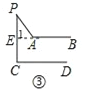
如图③,延长BA交PC于E,
∵AB∥CD,
∴∠1=∠C,
∴∠1=∠C=∠BAP﹣∠P;
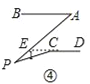
如图④,
延长CD交AP于E,
∵AB∥CD,
∴∠A=∠AEC=∠P+,
∴∠PCD=∠P+180°﹣∠A.
故答案为:∠A+∠P,∠BAP﹣∠P,∠P+180°﹣∠A.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目



