题目内容
已知一元二次方程ax2+bx+c=0两根为x1,x2,x2+x1=- ,x2.x1=
,x2.x1= .如果抛物线y=ax2+bx+c经过点(1,2),若abc=4,且a≥b≥c,则|a|+|b|+|c|的最小值为
.如果抛物线y=ax2+bx+c经过点(1,2),若abc=4,且a≥b≥c,则|a|+|b|+|c|的最小值为
- A.5
- B.6
- C.7
- D.8
B
分析:易知:b+c=2-a,bc=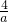 ,可将b、c看做是一元二次方程x2-(2-a)x+
,可将b、c看做是一元二次方程x2-(2-a)x+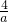 =0的两实根,那么可根据△≥0,求得a的大致取值范围为a≥4.由于abc=4>0,且a≥b≥c,则说明:
=0的两实根,那么可根据△≥0,求得a的大致取值范围为a≥4.由于abc=4>0,且a≥b≥c,则说明:
①a、b、c均大于0,由于a≥4,如果三数均为正数,显然a+b+c>4≠2,因此不合题意.
②a正,b、c为负,那么此时|a|+|b|+|c|=a-(b+c)=a-(2-a)=2a-2,根据得出的a的取值范围,即可求出|a|+|b|+|c|的最小值.
解答:∵a≥b≥c,若a<0,则b<0,c<0,a+b+c<0,与a+b+c=2矛盾,
∴a>0;
∵b+c=2-a,bc=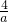 ,
,
∴b,c是一元二次方程x2-(2-a)x+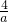 =0的两实根.
=0的两实根.
∴△=(2-a)2-4×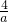 ≥0,
≥0,
∴a3-4a2+4a-16≥0,即(a2+4)(a-4)≥0,故a≥4.
∵abc>0,
∴a,b,c为全大于0或一正二负.
①若a,b,c均大于0,
∵a≥4,与a+b+c=2矛盾;
②若a,b,c为一正二负,则a>0,b<0,c<0,
则|a|+|b|+|c|=a-b-c=a-(2-a)=2a-2,
∵a≥4,
故2a-2≥6
当a=4,b=c=-1时,满足题设条件且使不等式等号成立.
故|a|+|b|+|c|的最小值为6.
故选B.
点评:本题主要考查了二次函数与一元二次方程的关系、韦达定理的应用及不等式的相关知识.
分析:易知:b+c=2-a,bc=
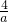 ,可将b、c看做是一元二次方程x2-(2-a)x+
,可将b、c看做是一元二次方程x2-(2-a)x+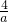 =0的两实根,那么可根据△≥0,求得a的大致取值范围为a≥4.由于abc=4>0,且a≥b≥c,则说明:
=0的两实根,那么可根据△≥0,求得a的大致取值范围为a≥4.由于abc=4>0,且a≥b≥c,则说明:①a、b、c均大于0,由于a≥4,如果三数均为正数,显然a+b+c>4≠2,因此不合题意.
②a正,b、c为负,那么此时|a|+|b|+|c|=a-(b+c)=a-(2-a)=2a-2,根据得出的a的取值范围,即可求出|a|+|b|+|c|的最小值.
解答:∵a≥b≥c,若a<0,则b<0,c<0,a+b+c<0,与a+b+c=2矛盾,
∴a>0;
∵b+c=2-a,bc=
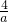 ,
,∴b,c是一元二次方程x2-(2-a)x+
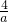 =0的两实根.
=0的两实根.∴△=(2-a)2-4×
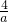 ≥0,
≥0,∴a3-4a2+4a-16≥0,即(a2+4)(a-4)≥0,故a≥4.
∵abc>0,
∴a,b,c为全大于0或一正二负.
①若a,b,c均大于0,
∵a≥4,与a+b+c=2矛盾;
②若a,b,c为一正二负,则a>0,b<0,c<0,
则|a|+|b|+|c|=a-b-c=a-(2-a)=2a-2,
∵a≥4,
故2a-2≥6
当a=4,b=c=-1时,满足题设条件且使不等式等号成立.
故|a|+|b|+|c|的最小值为6.
故选B.
点评:本题主要考查了二次函数与一元二次方程的关系、韦达定理的应用及不等式的相关知识.

练习册系列答案
相关题目
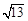 时,求出此二次函数的解析式;
时,求出此二次函数的解析式;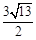 ,若存在求出P点坐标,若不存在请说明理由.
,若存在求出P点坐标,若不存在请说明理由. 时,求出此二次函数的解析式;
时,求出此二次函数的解析式;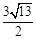 ,若存在求出P点坐标,若不存在请说明理由.
,若存在求出P点坐标,若不存在请说明理由.