题目内容
下表给出了变量x与ax2、ax2+bx+c之间的部分对应关系(表格中的符号“--”表示该项数据已经丢失):| x | -1 | 1 | |
| ax2 | -- | -- | 1 |
| ax2+bx+c | 7 | 2 | -- |
【答案】分析:根据表格的第2、3列得到a与c的值,把x=-1,以及a与c的值代入ax2+bx+c=7中即可求出b的值,由求出的a,b及c的值得到函数y=ax2+bx+c的关系式,然后利用配方法把抛物线的一般式变为顶点式,即可得到二次函数的顶点坐标.
解答:解:
根据题意,得a=1,c=2,a-b+c=7,解得b=-4.(3分)
所以所求函数的关系式为y=x2-4x+2.(4分)
配方得y=(x-2)2-2,(6分)
所以函数y=x2-4x+2图象的顶点坐标为(2,-2).(7分)
点评:此题考查学生从表格中提取信息的能力,会利用待定系数法求函数的解析式,会根据二次函数的解析式求函数图象的顶点坐标,是一道中档题.此题求顶点坐标的方法可以直接利用顶点坐标公式(- ,
, )来求.
)来求.
解答:解:
根据题意,得a=1,c=2,a-b+c=7,解得b=-4.(3分)
所以所求函数的关系式为y=x2-4x+2.(4分)
配方得y=(x-2)2-2,(6分)
所以函数y=x2-4x+2图象的顶点坐标为(2,-2).(7分)
点评:此题考查学生从表格中提取信息的能力,会利用待定系数法求函数的解析式,会根据二次函数的解析式求函数图象的顶点坐标,是一道中档题.此题求顶点坐标的方法可以直接利用顶点坐标公式(-
 ,
, )来求.
)来求. 
练习册系列答案
相关题目
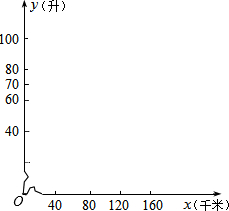
张师傅驾车在高速公路的A处加满油后,以某一均匀的速度从南方前往北方运送荔枝,下表记录的是货车一次加满油后油箱内剩余油量y(升)与行驶路程x(千米)之间的关系:
(1)请你在所给的平面直角坐标系中,以行驶路程x(千米)为横坐标,油箱内剩余油量y(升)为纵坐标描出各点;
(2)观察这些点的发展趋势,用你学过的正比例函数或一次函数来表示y与x之间的变化规律,说明选择这种函数的理由,并求出它的函数表达式;(不要求写出自变量的取值范围)
(3)货车从A处出发到达B处时行驶了336千米,求此时油箱内剩余的油量.
| 行驶路程x(千米) | 0 | 80 | 120 | 160 |
| 剩余油量y(升) | 100 | 80 | 70 | 60 |
(2)观察这些点的发展趋势,用你学过的正比例函数或一次函数来表示y与x之间的变化规律,说明选择这种函数的理由,并求出它的函数表达式;(不要求写出自变量的取值范围)
(3)货车从A处出发到达B处时行驶了336千米,求此时油箱内剩余的油量.

下表给出了变量x与ax2、ax2+bx+c之间的部分对应关系(表格中的符号“--”表示该项数据已经丢失):
| x | -1 | 0 | 1 |
| ax2 | -- | -- | 1 |
| ax2+bx+c | 7 | 2 | -- |
张师傅驾车在高速公路的A处加满油后,以某一均匀的速度从南方前往北方运送荔枝,下表记录的是货车一次加满油后油箱内剩余油量y(升)与行驶路程x(千米)之间的关系:
| 行驶路程x(千米) | 0 | 80 | 120 | 160 |
| 剩余油量y(升) | 100 | 80 | 70 | 60 |
(2)观察这些点的发展趋势,用你学过的正比例函数或一次函数来表示y与x之间的变化规律,说明选择这种函数的理由,并求出它的函数表达式;(不要求写出自变量的取值范围)
(3)货车从A处出发到达B处时行驶了336千米,求此时油箱内剩余的油量.
