Question

【题目】如图，在四边形中，,,,，连接,点是在四边形边上的一点；若点到的距离为 ，这样的点有 （ ）

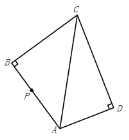
A. 0个B. 1个C. 2个D. 3个

Answer 1

【答案】D

【解析】

作DE⊥AC，垂足为E,得出 即点与重合.除外边的其它点到的距离都小于；假设在边存在一个点使时,根据等腰三角形和直角三角形的相关性质可以求出,由于AP=,这样满足条件的点在边是存在的.同理可得边也是存在的这样满足条件的点,所以符合条件的点共有3个；

∵,

∴,

∵,

∴,

按如图方式作于,

∴△ =,即,

∴ 即点与重合.除外边的其它点到的距离都小于,

假设在边存在一个点使（见示意图）时,根据等腰三角形和直角三角形的相关性质可以求出,

∴ ,

∵,

∴,

∴这样满足条件的点在边是存在的.同理可得边也是存在的这样满足条件的点,所以符合条件的点共有3个；

故选：D.