题目内容
计算:
(1)解方程组:
(2)解不等式
≤
+1,并将它的解集在数轴上表示出来.
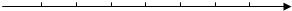
(3)解不等式组
,并写出该不等式组的整数解.
(1)解方程组:
|
(2)解不等式
| 4+3x |
| 6 |
| 1+2x |
| 3 |
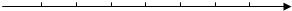
(3)解不等式组
|
分析:(1)先用加减消元法求出x的值,再用代入消元法求出y的值即可;
(2)先去分母,再去括号、移项、合并同类项,把x的系数化为1,再在数轴上表示出不等式的解集;
(3)分别求出各不等式的解集,再求出其公共解集,在其公共解集内找出x的整数解即可.
(2)先去分母,再去括号、移项、合并同类项,把x的系数化为1,再在数轴上表示出不等式的解集;
(3)分别求出各不等式的解集,再求出其公共解集,在其公共解集内找出x的整数解即可.
解答:解:(1)
,
①×2-②得,x=3;
把x=3代入①得,6-y=8,解得y=-2,
故此方程组的解为
;
(2)去分母得,4+3x≤2(1+2x)+1,
去括号得,4+3x≤2+4x+1,
移项得,3x-4x≤1-4,
系数化为1得,x≥-4,
在数轴上表示为:
 ;
;
(3)
,由不等式①得,x≥-4;由不等式②得,x<-1,
故此不等式组的解集为:-4≤x<-1.
故不等式组的整数解为:-4,-3,-2.
|
①×2-②得,x=3;
把x=3代入①得,6-y=8,解得y=-2,
故此方程组的解为
|
(2)去分母得,4+3x≤2(1+2x)+1,
去括号得,4+3x≤2+4x+1,
移项得,3x-4x≤1-4,
系数化为1得,x≥-4,
在数轴上表示为:
 ;
;(3)
|
故此不等式组的解集为:-4≤x<-1.
故不等式组的整数解为:-4,-3,-2.
点评:本题考查的是解二元一次不等式组及解二元一次方程组,熟知解二元一次不等式组的基本步骤是解答此题的关键.

练习册系列答案
相关题目
 (2)解方程组:
(2)解方程组: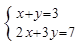 .
.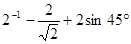 (2)解方程组:
(2)解方程组: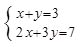 .
.