题目内容
(2000•山西)若将一个半径为80cm,面积为3200πcm2的扇形围成一个圆锥(围成圆锥后的接缝不计),则它的高是 cm.
【答案】分析:先根据扇形的面积公式计算出扇形的圆心角,再利用周长公式计算出底面圆的周长,得出半径.再构建直角三角形,解直角三角形即可.
解答: 解:3200π=
解:3200π=
解得n=180°
∴扇形的弧长= =80πcm.
=80πcm.
围成一个圆锥后如图所示:
因为扇形弧长=圆锥底面周长
即80π=2πr
解得r=40cm,即OB=40cm
根据勾股定理得OC=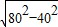 =40
=40 cm.
cm.
点评:本题综合考查了弧长公式,扇形弧长=用它围成的圆锥底面周长,及勾股定理等知识,所以学生学过的知识一定要结合起来.
解答:
 解:3200π=
解:3200π=
解得n=180°
∴扇形的弧长=
 =80πcm.
=80πcm.围成一个圆锥后如图所示:
因为扇形弧长=圆锥底面周长
即80π=2πr
解得r=40cm,即OB=40cm
根据勾股定理得OC=
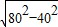 =40
=40 cm.
cm.点评:本题综合考查了弧长公式,扇形弧长=用它围成的圆锥底面周长,及勾股定理等知识,所以学生学过的知识一定要结合起来.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

