题目内容
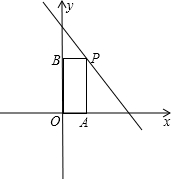 如图,在一次函数y=-x+3的图象上取点P,作PA⊥x轴,PB⊥y轴;垂足为B,且矩形OAPB的面积为2,则这样的点P个数共有( )
如图,在一次函数y=-x+3的图象上取点P,作PA⊥x轴,PB⊥y轴;垂足为B,且矩形OAPB的面积为2,则这样的点P个数共有( )| A、1 | B、2 | C、3 | D、4 |
分析:设P(x,y).根据题意,得|xy|=2,即xy=±2,然后分别代入一次函数,即可得P点的个数.
解答:解:设P(x,y).根据题意,得|xy|=2,即xy=±2
当xy=2时,把y=-x+3代入,得:x(-x+3)=2,即x2-3x+2=0,解得:x=1或x=2,则P(1,2)或(2,1)
当xy=-2时,把y=-x+3代入,得:x(-x+3)=-2,即x2-3x-2=0,解得:x=
则P(
,
)或(
,
).
故选D.
当xy=2时,把y=-x+3代入,得:x(-x+3)=2,即x2-3x+2=0,解得:x=1或x=2,则P(1,2)或(2,1)
当xy=-2时,把y=-x+3代入,得:x(-x+3)=-2,即x2-3x-2=0,解得:x=
3±
| ||
| 2 |
则P(
3+
| ||
| 2 |
3-
| ||
| 2 |
3-
| ||
| 2 |
3+
| ||
| 2 |
故选D.
点评:此题要用设坐标的方法求解,注意坐标与线段长度的区别,分情况讨论,同时要熟练解方程组.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
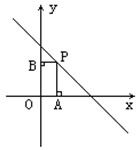 8、如图,在一次函数y=-x+5的图象上取点P,作PA⊥x轴,PB⊥y轴;垂足为B,且矩形OAPB的面积为6,则这样的点P个数共有( )
8、如图,在一次函数y=-x+5的图象上取点P,作PA⊥x轴,PB⊥y轴;垂足为B,且矩形OAPB的面积为6,则这样的点P个数共有( )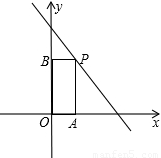
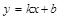 中,若
中,若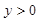 ,则( )
,则( )
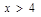 B、
B、
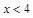 C、
C、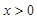 D、
D、