题目内容
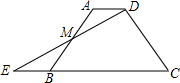 (自编题)梯形ABCD中,AD∥BC,延长CB至E,使BE=AD.
(自编题)梯形ABCD中,AD∥BC,延长CB至E,使BE=AD.(1)求证:M为AB的中点.
(2)用直尺作出CD的中点N,并在图上标上理由.连AN交DE于O,设AD=3,BC=5.求
| DO | OE |
分析:(1)证明△ADM≌△BEM(AAS),由全等三角形的性质即可得到DM=EM,即M为AB的中点.
(2)作CD的垂直平分线,交CD于点N,点N即为所求;
(2)作CD的垂直平分线,交CD于点N,点N即为所求;
解答:(1)证明:∵AD∥BC,
∴∠ADM=∠E,
在△AMD和△BME中,
,
∴△ADM≌△BEM(AAS),
∴DM=EM,
即M为AB的中点.
(2)如图:作CD的垂直平分线,交CD于点N,点N即为所求;
解:延长BC到F,连接FN,则AD=CF,
∵△ADM≌△BEM,
∴AD=BE,
∴EF=EB+BC+CF=3+3+5=11,
∵AD∥BC,
∴△AOD∽△FOE,
∴AD:EF=DO:OE=3:11,
∴
=
.
∴∠ADM=∠E,
在△AMD和△BME中,
|
∴△ADM≌△BEM(AAS),
∴DM=EM,

即M为AB的中点.
(2)如图:作CD的垂直平分线,交CD于点N,点N即为所求;
解:延长BC到F,连接FN,则AD=CF,
∵△ADM≌△BEM,
∴AD=BE,
∴EF=EB+BC+CF=3+3+5=11,
∵AD∥BC,
∴△AOD∽△FOE,
∴AD:EF=DO:OE=3:11,
∴
| DO |
| OE |
| 3 |
| 11 |
点评:本题考查了全等三角形的判定和性质、梯形的性质、相似三角形的判定和性质、垂直平分线的作法,题目的综合性强,难度中等.

练习册系列答案
相关题目

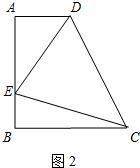
 26、如图1,在正方形ABCD中,若点E是△DBC内的一点,且DE=DC,BE=CE.
26、如图1,在正方形ABCD中,若点E是△DBC内的一点,且DE=DC,BE=CE.