题目内容
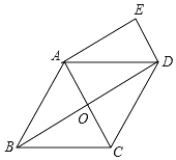
【题目】已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
(1)求证:四边形AODE是矩形;
(2)若AB=![]() ,∠BCD=120°,连接CE,求CE的长.
,∠BCD=120°,连接CE,求CE的长.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)首先根据菱形的性质,可得AC⊥BD,然后判断出四边形AODE是平行四边形,即可推得四边形AODE是矩形.
(2)在Rt△AEC中,求出AC、AE即可解决问题.
(1)证明:∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠AOD=90°,
又∵DE∥AC,AE∥BD,
∴四边形AODE是平行四边形,
∴四边形AODE是矩形.
(2)∵∠BCD=120°,四边形ABCD是菱形,
∴∠BAD=∠BCD=120°,∠CAB=∠CAD=60°,AB=BC,
∴△ABC是等边三角形,
∴AC=AB=2![]() ,OB=OD=AE=3,
,OB=OD=AE=3,
在Rt△AEC中,EC=![]() =
=![]() =
=![]() .
.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目