题目内容
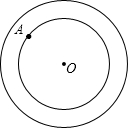（2012•台湾）如图，大、小两圆的圆心均为O点，半径分别为3、2，且A点为小圆上的一固定点．若在大圆上找一点B，使得OA=AB，则满足上述条件的B点共有几个？（ ）分析：由题意可得连接OA，以A点为圆心，OA为半径画弧，交大圆于B1、B2两点，则可得满足上述条件的B点共有2个．
解答：
解：连接OA，以A点为圆心，OA为半径画弧，交大圆于B1、B2两点，
则B1、B2即为所求（AB1=AB2=OA）．
即满足条件的B点共有2个．
故选C．
解：连接OA，以A点为圆心，OA为半径画弧，交大圆于B1、B2两点，则B1、B2即为所求（AB1=AB2=OA）．
即满足条件的B点共有2个．
故选C．
点评：此题考查了圆与圆的位置关系．此题难度适中，解此题的关键是数形结合思想的应用，注意由OA=AB，可得点B位于以A为圆心，OA长为半径的圆上．
练习册系列答案
寒假大串联黄山书社系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
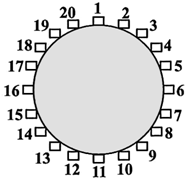（2012•台湾）如图，一圆桌周围有20个箱子，依顺时针方向编号1～20．小明在1号箱子中丢入一颗红球后，沿着圆桌依顺时针方向行走，每经过一个箱子就依下列规则丢入一颗球：
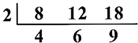（2012•台湾）如图是利用短除法求出三数8、12、18的最大公因子的过程．利用短除法，求出这三数的最小公倍数为何？（ ）
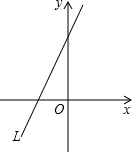（2012•台湾）如图，坐标平面上直线L的方程式为3x-y=-3．若有一直线L′的方程式为y=a，则a的值在下列哪一个范围时，L′与L的交点会在第二象限？（ ）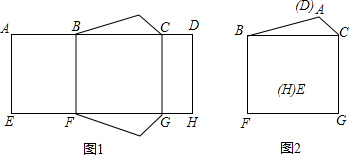
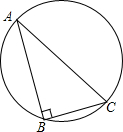（2012•台湾）如图，直角三角形ABC有一外接圆，其中∠B=90°，AB＞BC，今欲在