题目内容
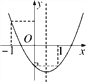
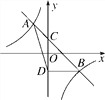
【题目】如图,一次函数y=k1x+b与反比例函数y=![]() (k2≠0)相交于A(-1,2),B(2,m)两点,与y轴相交于点C.
(k2≠0)相交于A(-1,2),B(2,m)两点,与y轴相交于点C.
(1)求k1、k2、m的值;
(2)若点D与点C关于x轴对称,求△ABD的面积;
(3)若M(x1,y1)、N(x2、y2)是反比例函数y=![]() 图象上的两点,且x1<x2时,y1>y2,指出点M、N各位于坐标系的哪个象限,并简要说明理由.
图象上的两点,且x1<x2时,y1>y2,指出点M、N各位于坐标系的哪个象限,并简要说明理由.
【答案】(1)![]() ;(2) 3;(3)当点M在第二象限,点N在第四象限时,满足当x1<x2时,y1>y2.
;(2) 3;(3)当点M在第二象限,点N在第四象限时,满足当x1<x2时,y1>y2.
【解析】(1)把A的坐标代入y=![]() 即可求得k2,得到反比例函数的解析式,再把B(2,m)代入反比例函数的解析式即可求得m的值,然后根据待定系数法即可求得k1;
即可求得k2,得到反比例函数的解析式,再把B(2,m)代入反比例函数的解析式即可求得m的值,然后根据待定系数法即可求得k1;
(2)根据一次函数的解析式求得点C的坐标,根据题意求得D的坐标,从而求得DB∥x轴,BD=2,然后根据三角形,、面积公式求得即可;
(3)根据反比例函数的性质即可判断.
(1)∵比例函数y=![]() 经过A(-1,2),
经过A(-1,2),
∴k2=-2,
∴比例函数为y=-![]() ,
,
∵B(2,m)在比例函数y=-![]() 的图象上,
的图象上,
∴m=-![]() =-1,
=-1,
∴B(2,-1),
∵直线y=k1x+b经过A(-1,2),B(2,-1),
∴![]() ,解得k1=-1,b=1,
,解得k1=-1,b=1,
(2)由直线y=-x+1可知C(0,1),
∵点D与点C关于x轴对称,
∴D(0,-1),
∵B(2,-1),
∴BD∥x轴,BD=2,
∴△ABD的面积=![]() ×2×(2+1)=3;
×2×(2+1)=3;
(3)点M位于第二象限,N位于第四象限,
∵k2=-2<0,图象位于二、四象限,在每个象限内,y随x的增大而增大,
∴如果M(x1,y1)、N(x2,y2)位于同一象限,有且x1<x2时,则y1<y2,
∴M(x1,y1)、N(x2,y2)位于不同的象限,
∵x1<x2,
∴点M位于第二象限,N位于第四象限.

 阅读快车系列答案
阅读快车系列答案