题目内容
 (2013•枣庄)已知矩形ABCD中,AB=1,在BC上取一点E,AE将△ABE向上折叠,使B点落在AD上的F点.若四边形EFDC与矩形ABCD相似,则AD=
(2013•枣庄)已知矩形ABCD中,AB=1,在BC上取一点E,AE将△ABE向上折叠,使B点落在AD上的F点.若四边形EFDC与矩形ABCD相似,则AD=
| ||
| 2 |
| ||
| 2 |
分析:可设AD=x,由四边形EFDC与矩形ABCD相似,根据相似多边形对应边的比相等列出比例式,求解即可.
解答:解:∵AB=1,
设AD=x,则FD=x-1,FE=1,
∵四边形EFDC与矩形ABCD相似,
∴
=
,
=
,
解得x1=
,x2=
(不合题意舍去),
经检验x1=
是原方程的解.
故答案为
.
设AD=x,则FD=x-1,FE=1,
∵四边形EFDC与矩形ABCD相似,
∴
| EF |
| FD |
| AD |
| AB |
| 1 |
| x-1 |
| x |
| 1 |
解得x1=
| ||
| 2 |
1-
| ||
| 2 |
经检验x1=
| ||
| 2 |
故答案为
| ||
| 2 |
点评:本题考查了翻折变换(折叠问题),相似多边形的性质,本题的关键是根据四边形EFDC与矩形ABCD相似得到比例式.

练习册系列答案
相关题目
 (2013•枣庄)校车安全是近几年社会关注的重大问题,安全隐患主要是超速和超载.某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点C,再在笔直的车道l上确定点D,使CD与l垂直,测得CD的长等于21米,在l上点D的同侧取点A、B,使∠CAD=30°,∠CBD=60°.
(2013•枣庄)校车安全是近几年社会关注的重大问题,安全隐患主要是超速和超载.某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点C,再在笔直的车道l上确定点D,使CD与l垂直,测得CD的长等于21米,在l上点D的同侧取点A、B,使∠CAD=30°,∠CBD=60°. (2013•枣庄)如图,已知线段OA交⊙O于点B,且OB=AB,点P是⊙O上的一个动点,那么∠OAP的最大值是( )
(2013•枣庄)如图,已知线段OA交⊙O于点B,且OB=AB,点P是⊙O上的一个动点,那么∠OAP的最大值是( )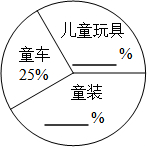 (2013•枣庄)“六•一”前夕,质检部门从某超市经销的儿童玩具、童车和童装中共抽查了300件儿童用品.以下是根据抽查结果绘制出的不完整的统计表和扇形图:
(2013•枣庄)“六•一”前夕,质检部门从某超市经销的儿童玩具、童车和童装中共抽查了300件儿童用品.以下是根据抽查结果绘制出的不完整的统计表和扇形图: