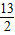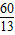题目内容
已知BC是半径为2cm的圆内的一条弦,点A为圆上除点B、C外任意一点,若BC= cm,则∠BAC的度数为 .
cm,则∠BAC的度数为 .
【答案】分析:作OD⊥BC,垂足为D,由垂径定理知,点D是BC的中点,易得sin∠BOD=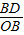 =
=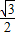 ,所以可求∠BOD=60°,∠BOC=120°,
,所以可求∠BOD=60°,∠BOC=120°,
分别求出当点A在优弧上时∠A的度数,当点A在如图点E位置时E的度数,即可知道∠BAC的度数为60°或120°.
解答: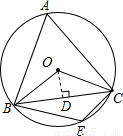 解:如图.作OD⊥BC,垂足为D.
解:如图.作OD⊥BC,垂足为D.
∵点D是BC的中点,BD= BC=
BC=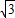 ,
,
∴sin∠BOD=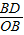 =
=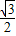 .
.
∴∠BOD=60°.∠BOC=120°.
当点A在优弧上时,由圆周角定理知,∠A= ∠BOC=60°;
∠BOC=60°;
当点A在如图点E位置时,由圆内接四边形的对角互补知,∠E=180°-∠A=120°.
∴∠BAC的度数为60°或120°.
点评:本题利用了圆内接四边形的性质和圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.注意点A的位置有两种情况.
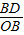 =
=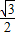 ,所以可求∠BOD=60°,∠BOC=120°,
,所以可求∠BOD=60°,∠BOC=120°,分别求出当点A在优弧上时∠A的度数,当点A在如图点E位置时E的度数,即可知道∠BAC的度数为60°或120°.
解答:
 解:如图.作OD⊥BC,垂足为D.
解:如图.作OD⊥BC,垂足为D.∵点D是BC的中点,BD=
 BC=
BC=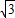 ,
,∴sin∠BOD=
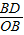 =
=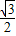 .
.∴∠BOD=60°.∠BOC=120°.
当点A在优弧上时,由圆周角定理知,∠A=
 ∠BOC=60°;
∠BOC=60°;当点A在如图点E位置时,由圆内接四边形的对角互补知,∠E=180°-∠A=120°.
∴∠BAC的度数为60°或120°.
点评:本题利用了圆内接四边形的性质和圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.注意点A的位置有两种情况.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知在Rt△ABC中,∠A=90°,两直角边分别为5,12,以A为圆心与BC相切的圆半径是( )
A、
| ||
| B、2 | ||
C、
| ||
| D、5 |