题目内容
已知在Rt△ABC中，∠A=90°，两直角边分别为5，12，以A为圆心与BC相切的圆半径是（ ）
A、
| ||
| B、2 | ||
C、
| ||
| D、5 |
分析：根据切线的性质，得出AD⊥BC，再利用三角形面积即可得出．
解答：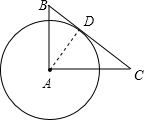
解：根据题意画出图象，假设以A为圆心与BC相切于点D，
连接AD，∵两直角边分别为5，12，以A为圆心与BC相切，
∴AD⊥BC，
∴AB×AC=AD×BC，
∵AB=5，BC=12，BC=13，
∴AD=
，
故选：C．
解：根据题意画出图象，假设以A为圆心与BC相切于点D，连接AD，∵两直角边分别为5，12，以A为圆心与BC相切，
∴AD⊥BC，
∴AB×AC=AD×BC，
∵AB=5，BC=12，BC=13，
∴AD=
| 60 |
| 13 |
故选：C．
点评：此题主要考查了切线的性质定理，根据已知得出AB×AC=AD×BC是解决问题的关键．
练习册系列答案
中考利剑中考试卷汇编系列答案
教育世家状元卷系列答案
黄冈课堂作业本系列答案
相关题目
如图，已知在Rt△ABC中，∠ACB=90°，AB=4，分别以AC，BC为直径作半圆，面积分别记为S1，S2，则S1+S2的值等于（ ）
（1）已知在Rt△ABC中，∠C=90°，sinA=