题目内容
如图,数在线的A、B、C、D四点所表示的数分别为a、b、c、d,且O为原点.根据图中各点位置,判断|a﹣c|之值与下列何者不同?( )
![]()
|
| A. | |a|+|b|+|c| | B. | |a﹣b|+|c﹣b| | C. | |a﹣d|﹣|d﹣c| | D. | |a|+|d|﹣|c﹣d| |
考点:
实数与数轴。
专题:
探究型。
分析:
根据绝对值的性质计算出各绝对值表示的线段长,与|a﹣c|的长进行比较即可.
解答:
解:A、∵|a|+|b|+|c|=AO+BO+CO≠AC,故本选项正确;
B、∵|a﹣b|+|c﹣b|=AB+BC=AC,故本选项错误;
C、∵|a﹣d|﹣|d﹣c|=AD﹣CD=AC,故本选项错误;
D、∵|a|+|d|﹣|c﹣d|=AO+DO﹣CD=AC,故本选项错误;
故选A.
点评:
本题考查了实数与数轴,知道绝对值的意义是解题的关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
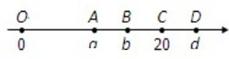
 (2012•台湾)如图,数在线的A、B、C、D四点所表示的数分别为a、b、c、d,且O为原点.根据图中各点位置,判断|a-c|之值与下列何者不同?( )
(2012•台湾)如图,数在线的A、B、C、D四点所表示的数分别为a、b、c、d,且O为原点.根据图中各点位置,判断|a-c|之值与下列何者不同?( )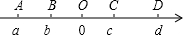 如图,数在线的A、B、C、D四点所表示的数分别为a、b、c、d,且O为原点.根据图中各点位置,判断|a-c|之值与下列何者不同?
如图,数在线的A、B、C、D四点所表示的数分别为a、b、c、d,且O为原点.根据图中各点位置,判断|a-c|之值与下列何者不同?