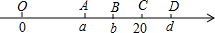题目内容
5、如图所示，数在线的A、B、C、D四点所表示的数分别a、b、20、d．若a、b、20、d为等差数列，且|a-d|=12，则a值（ ）
分析：首先由图可知a＜b＜20＜d，则|a-d|=d-a，再根据a、b、20、d为等差数列，由等差数列的定义，如果设公差为m，则d-20=20-b=b-a=m，根据|a-d|=12，可求出m，进而得出a的值．
解答：解：由图可知a＜b＜20＜d，∴|a-d|=d-a=12，
∵a、b、20、d为等差数列，设公差为m，则d-20=20-b=b-a=m，
∴d=a+3m，
∴d-a=3m=12，
∴m=4，
∴d=20+m=24，
∴a=d-12=12．
故选B．
∵a、b、20、d为等差数列，设公差为m，则d-20=20-b=b-a=m，
∴d=a+3m，
∴d-a=3m=12，
∴m=4，
∴d=20+m=24，
∴a=d-12=12．
故选B．
点评：本题主要考查了等差数列的有关定义及通项公式．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
