题目内容
【题目】如图,△OAB是边长为2的等边三角形,过点A的直线![]()
(1)求点E的坐标;
(2)求证OA⊥AE.
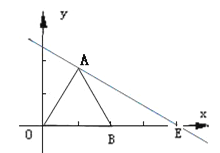
【答案】(1)点E(4,0)。(2)证明见解析
【解析】试题分析:(1)利用等边三角形的性质得出OD=BD=1,再利用勾股定理得出AD的长,即可得出A点坐标,即可求出函数解析式;
(2)利用E点坐标得出EO的长,进而求出AE的长,再利用勾股定理逆定理得出答案.
试题解析:
(1)解:过点A作AD⊥EO于点D,
∵△OAB是边长为2的等边三角形,
∴OD=DB=1,AB=AO=OB=2,
∴AD=![]() ,
,
∴A(1,![]() ),
),
将A点代入直线y=-![]() 得:
得:
![]() ,
,
解得:m=![]() ,
,
∴y=-![]() ,
,
则y=0时,x=4,
即E(4,0);
(2) 证明:∵AD=![]() ,DE=EO-DO=3,
,DE=EO-DO=3,
∴AE=![]() ,
,
∵AO2+AE2=16,EO2=16,
∴AO2+AE2=EO2,
∴OA⊥AE.

练习册系列答案
相关题目
【题目】在禁毒知识考试中,全班同学的成绩统计如下表:
得分(分) | 60 | 70 | 80 | 90 | 100 |
人数(人) | 7 | 22 | 10 | 8 | 3 |
则得分的众数和中位数分别为( )
A. 70分,70分B. 80分,80分C. 70分,80分D. 80分,70分