Question

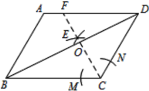
【题目】已知：如图，在平行四边形ABCD中，对角线AC与BD交于点O，点E是DB延长线上的一点，且EA＝EC，分别延长AD、EC交于点F．

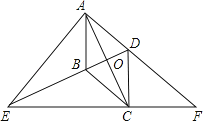
（1）求证：四边形ABCD为菱形；

（2）如果∠AEC＝2∠BAC，求证：ECCF＝AFAD．

Answer 1

【答案】（1）见解析；（2）见解析

【解析】

（1）由四边形ABCD是平行四边形知OA＝OC，结合EA＝EC知EO⊥AC，从而得证；

（2）先由∠AEB＝∠CEB＝∠AEC，平行四边形ABCD为菱形得∠CDF＝∠DAC+∠DCA＝∠AEF，据此可证△FCD∽△FAE得，结合CD＝AD，AE＝CE可得答案．

（1）∵四边形ABCD是平行四边形，

∴OA＝OC，

又∵EA＝EC，

∴EO⊥AC，

∴四边形ABCD是菱形；

（2）∵∠AEB＝∠CEB＝∠AEC，平行四边形ABCD为菱形，

∴∠AEB＝∠CEB＝∠BAC＝∠BCA＝∠DAC＝∠DCA，

∠CDF＝∠DAC+∠DCA＝∠AEF，

∴△FCD∽△FAE，

∴，
∵CD=AD，AE=CE，
∴ ，即ECCF=AFAD．