Question

【题目】问题原型：如图①，正方形ABCD的对角线交于点O，点E、F分别为边AB、AD中点，且∠EOF=90°，易得四边形AEOF的面积是正方形ABCD的面积的四分之一．（不用证明）

探究发现：某数学兴趣小组，尝试改变点E、F的位置，点E、F分别为边AB、AD上任一点，且∠EOF=90°，如图②，探究：四边形AEOF的面积是否为正方形ABCD面积的四分之一？并说明理由．
拓展提升：如图③，菱形ABCD中，∠BAD=120°，∠EAF=60°，且点E、F分别在边DC、BC上，四边形AECF的面积是菱形ABCD面积的几分之一？（直接写出结果即可）

Answer 1

【答案】解：探究发现，四边形AEOF的面积是否为正方形ABCD面积的四分之一．

理由：如图②中，

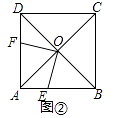
∵四边形ABCD是正方形，

∴DO=AO，∠ODF=∠OAE=45°，∠DOA=90°，△AOD的面积是正方形ABCD面积的四分之一，

∵∠EOF=90°，

∴∠AOE+∠AOF=90°，又∠ODF=∠AOF=∠DOA=90°，

∴∠AOE=∠DOF，

∴△AOE≌△DOF，

∴S四边形AEOF=S△AOD，

∴S四边形AEOF= S正方形ABCD．

拓展提升：结论：S四边形AEGF= S菱形ABGD．

理由：如图③中，连接AG．

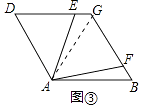
∵四边形ABGD是菱形，∠DAB=120°，

∴AB=BG=GD=AD，∠GAD=∠GAB=60°，

∴△ADG和△ABG都是等边三角形，

∴∠D=∠AGF=60°，AD=AG，

∵∠DAG=∠EAF=60°，

∴∠DAE=∠GAF，

∴△DAE≌△GAF，

∴S△DAE=S△GAF，

∴S四边形AEGF=S△ADG= S菱形ABGD．

【解析】探究发现：只要证明△AOE≌△DOF，可得S四边形AEOF=S△AOD，推出S四边形AEOF= S正方形ABCD；

拓展提升：结论：S四边形AEGF= S菱形ABGD．只要证明△DAE≌△GAF即可解决问题；