题目内容
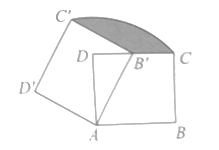
【题目】二次函数![]() 的图象如图所示,有下列结论:
的图象如图所示,有下列结论: ![]() ;
;![]() ;
;![]() 若m为任意实数,则
若m为任意实数,则![]() ;
;![]() ;
;![]() 若
若![]() ,且
,且![]() ,则
,则![]() 其中,正确结论的个数为
其中,正确结论的个数为![]()
A.4B.3C.2D.1
【答案】C
【解析】
由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解:①抛物线开口方向向下,则a<0.
抛物线对称轴位于y轴右侧,则a、b异号,即ab<0.
抛物线与y轴交于正半轴,则c>0
所以abc<0.
故①错误.
②∵抛物线对称轴为直线x=![]() ,
,
∴b=-2a,即2a+b=0,
故②正确;
③∵抛物线对称轴为直线x=1,
∴函数的最大值为:a+b+c,
∴当m≠1时,a+b+c>am2+bm+c,即a+b>am2+bm,
故③错误;
④∵抛物线与x轴的一个交点在(3,0)的左侧,而对称轴为直线x=1,
∴抛物线与x轴的另一个交点在(-1,0)的右侧
∴当x=-1时,y<0,
∴a-b+c<0,
故④错误;
⑤∵ax12+bx1=ax22+bx2,
∴ax12+bx1-ax22-bx2=0,
∴a(x1+x2)(x1-x2)+b(x1-x2)=0,
∴(x1-x2)[a(x1+x2)+b]=0,
而x1≠x2,
∴a(x1+x2)+b=0,即x1+x2=![]() ,
,
∵b=-2a,
∴x1+x2=2,
故⑤正确.
综上所述,正确的有②⑤.
故选:C.

 轻松暑假总复习系列答案
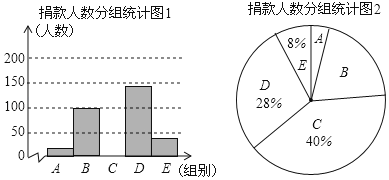
轻松暑假总复习系列答案【题目】某校学生会干部对全校师生倡导的“武汉加油”的自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,对学校部分捐款人数进行调查和分组统计后,将数据整理成如图所示的统计图(图中信息不完整).已知A、B两组捐款人数的比为1∶5.
组别 | 捐款额x(元) | 人数 |
A | 1≤x<10 | a |
B | 10≤x<20 | 100 |
C | 20≤x<30 | |
D | 30≤x<40 | |
E | 40≤x<50 |
请结合以上信息解答下列问题.
(1)a= ,本次调查样本的容量是 ;
(2)先求出C组的人数,再补全“捐款人数分组统计图1”;
(3)根据统计情况,估计该校参加捐款的5000名学生有多少人捐款在20至50元之间.
【题目】甲、乙两家商场平时以同样价格出售相同的商品.春节期间两家商场都让利酬宾,其中甲商场所有商品按8折出售,乙商场对一次购物中不超过200元的不打折,超过200元后的价格部分打7折.
设商品原价为x元,顾客购物金额为y元.
(I).根据题意,填写下表:
商品原价 | 100 | 150 | 250 | … |
甲商场购物金额(元) | 80 | … | ||
乙商场购物金额(元) | 100 | … |
(Ⅱ).分别就两家商场的让利方式写出y关于x的函数关系式;
(Ⅲ).若x≥500时,选择哪家商场去购物更省钱?并说明理由.
【题目】2020蓉漂云招聘活动在4月25日正式启动,共发布了岗位13198个.某网络公司招聘一名高级网络工程师,应聘者小魏参加笔试和面试,成绩(100分制)如表所示:
笔试 | 面试 | |||||||
成绩 | 98 | 评委1 | 评委2 | 评委3 | 评委4 | 评委5 | 评委6 | 评委 7 |
94 | 95 | 92 | 99 | 98 | 97 | 96 | ||
其中规定:面试得分中去掉一个最高分和一个最低分,余下的面试得分的平均值作为应聘者的面试成绩.
(1)请计算小魏的面试成绩;
(2)如果面试成绩与笔试成绩按6:4的比例确定,请计算出小魏的最终成绩.
【题目】为了解某地区企业信息化发展水平,从该地区中随机抽取50家企业调研,针对体现企业信息化发展水平的A和B两项指标进行评估,获得了它们的成绩(十分制),并对数据(成绩)进行整理、描述和分析.下面给出了部分信息.
a.A项指标成绩的频数分布直方图如下(数据分成6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ):
):
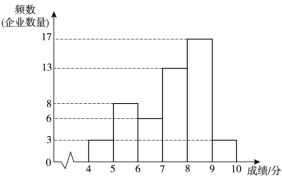
b.A项指标成绩在![]() 这一组的是:
这一组的是:
7.2 7.3 7.5 7.67 7.7 7.71 7.75 7.82 7.86 7.9 7.92 7.93 7.97
c.![]() 两项指标成绩的平均数、中位数、众数如下:
两项指标成绩的平均数、中位数、众数如下:
平均数 | 中位数 | 众数 | |
A项指标成绩 | 7.37 | m | 8.2 |
B项指标成绩 | 7.21 | 7.3 | 8 |
根据以上信息,回答下列问题:
(1)写出表中m的值
(2)在此次调研评估中,某企业A项指标成绩和B项指标成绩都是7.5分,该企业成绩排名更靠前的指标是______________(填“A”或“B”),理由是_____________;
(3)如果该地区有500家企业,估计A项指标成绩超过7.68分的企业数量.