题目内容
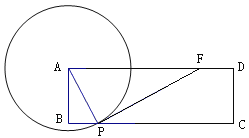
【题目】在矩形ABCD中,AB=3,BC=10,P是BC上的动点(不与B,C重合),以A为圆心,AP长为半径作圆A,若经过点P的圆A的切线与线段AD交于点F,则以DF,BP的长为对角线长的菱形的最大面积是( )
A. 4 B. 8 C. 12. 5 D. 16
【答案】B
【解析】过F作FE⊥CB于E,由∠B=∠E,∠BAP=∠EPF,得△BAP∽△EPF,
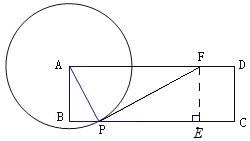
设BP=x,DF=y,则![]() ,
,![]() ,
,
∴9=x(10–x–y), xy= – x2+10x–9,
配方得到最大值为16.
即以DF,BP的长为对角线长的菱形的最大面积是8.
故选B.
“点睛”本题考查了切线的性质:圆心与切点的连线垂直切线,相似三角形的性质,解题时要运用数形结合的思想.

练习册系列答案
相关题目