题目内容
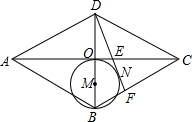 (2011•温州一模)如图,在菱形ABCD中,对角线AC,BD交于点O,以OB为直径画圆M,过D作⊙M的切线,切点为N,分别交AC,BC于点E,F,已知AE=5,CE=3,则DF的长是
(2011•温州一模)如图,在菱形ABCD中,对角线AC,BD交于点O,以OB为直径画圆M,过D作⊙M的切线,切点为N,分别交AC,BC于点E,F,已知AE=5,CE=3,则DF的长是4.8
4.8
.分析:延长EF,过B作直线平行AC和EF相交于P,先根据菱形的对角线互相平分得出OE=1,利用△DMN∽△DEO及MN=
DM,得出DE的长,进而利用中位线定理得出EP的长,再由△EFC∽△PFB,相似比是3:2,可得出EF的长,从而根据DF=DE+EF可求出DF的长度.
| 1 |
| 3 |
解答: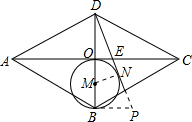 解:延长EF,过B作直线平行AC和EF相交于P,
解:延长EF,过B作直线平行AC和EF相交于P,
∵AE=5,EC=3,
∴AO=CE+OE,即有,OE=EN=1,
又∵△DMN∽△DEO,且MN=
DM,
∴DE=3OE=3,
又∵OE∥BP,O是DB中点,所以E也是中点,
∴EP=DE=3,
∴BP=2,
又∵△EFC∽△PFB,相似比是3:2,
∴EF=EP×
=1.8,
故可得DF=DE+EF=3+1.8=4.8.
故答案为:4.8.
 解:延长EF,过B作直线平行AC和EF相交于P,
解:延长EF,过B作直线平行AC和EF相交于P,∵AE=5,EC=3,
∴AO=CE+OE,即有,OE=EN=1,
又∵△DMN∽△DEO,且MN=
| 1 |
| 3 |
∴DE=3OE=3,
又∵OE∥BP,O是DB中点,所以E也是中点,
∴EP=DE=3,
∴BP=2,
又∵△EFC∽△PFB,相似比是3:2,
∴EF=EP×
| 3 |
| 5 |
故可得DF=DE+EF=3+1.8=4.8.
故答案为:4.8.
点评:此题考查了菱形的性质、相似三角形的判定及性质,及切线的性质,综合性较强,解答本题的关键是正确地作出辅助线,求出OE、DE的长,进而综合利用三角形的中位线定理求出EP,难度较大.

练习册系列答案
相关题目
 (2011•温州一模)由两个不同的长方体木块搭成的简易木凳如图所示,则它的主视图是( )
(2011•温州一模)由两个不同的长方体木块搭成的简易木凳如图所示,则它的主视图是( )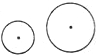 (2011•温州一模)如图,在纸上画出两个外离的圆,它们的半径分别为3cm和5cm,则圆心距可能是( )
(2011•温州一模)如图,在纸上画出两个外离的圆,它们的半径分别为3cm和5cm,则圆心距可能是( )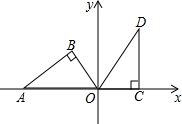 (2011•温州一模)如图,直角坐标系中,Rt△AOB的顶点A在x轴上,∠B=90°,OA=5,OB=3,现将△AOB绕原点O按顺时针方向旋转,得到△DOC,且点C在x轴上,则点D的坐标是( )
(2011•温州一模)如图,直角坐标系中,Rt△AOB的顶点A在x轴上,∠B=90°,OA=5,OB=3,现将△AOB绕原点O按顺时针方向旋转,得到△DOC,且点C在x轴上,则点D的坐标是( ) (2011•温州一模)如图,AB是⊙O的弦,C是
(2011•温州一模)如图,AB是⊙O的弦,C是