题目内容
如图，已知AB是⊙O的直径，CD是弦且CD⊥AB，BC＝6，AC=8,则sin∠ABD的值是（ ）
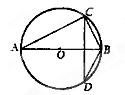
A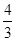． | B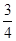． | C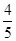． | D． |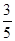
D
由垂径定理和圆周角定理可证∠ABD=∠ABC，再根据勾股定理求得AB=10，即可求sin∠ABD的值．
解：∵AB是⊙O的直径，CD⊥AB，
∴弧AC=弧AD，
∴∠ABD=∠ABC．
根据勾股定理求得AB=10，
∴sin∠ABD=sin∠ABC=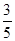
．
故选D．
此题综合考查了垂径定理以及圆周角定理的推论，熟悉锐角三角函数的概念．
解：∵AB是⊙O的直径，CD⊥AB，
∴弧AC=弧AD，
∴∠ABD=∠ABC．
根据勾股定理求得AB=10，
∴sin∠ABD=sin∠ABC=
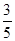．故选D．
此题综合考查了垂径定理以及圆周角定理的推论，熟悉锐角三角函数的概念．
练习册系列答案
相关题目
，∠AOC为( )
＝0.1736 , 
＝0.9848,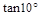 
＝0.1763.
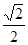,则△ABC是 三角形。
，AC=6cm，那么BC等于（▲）
