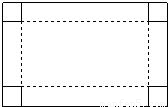
题目内容
有一张长比宽多8cm的矩形纸板.如果在纸板的四个角处各剪去一个正方形(如图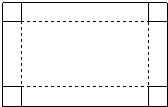 所示),可制成高是4cm,容积是512cm3的一个无盖长方体纸盒.
所示),可制成高是4cm,容积是512cm3的一个无盖长方体纸盒.(1)求矩形纸板的长和宽;
(2)在操作过程中,由于不小心,矩形纸板被剪掉一角,其直角边长分别为3cm和6cm.如果在剩余的纸板上先裁剪一个各边与原矩形纸板各边平行或重合的矩形,然后再按如图裁剪方式制作高仍是4cm的无盖长方体纸盒,那么你认为如何裁剪才能使制作的长方体纸盒的容积最大,请画出草图,并说明理由.
分析:(1)设出矩形纸板的宽,根据长比宽多8cm,即可表示出纸板的长,然后根据长方体纸盒的容积列方程求出纸板的长和宽.
(2)首先根据已知条件画出草图,设能够裁剪的矩形为CGHP,并延长GH交ND于M,由于HM∥AM,易证得△HME∽△ANE,可得关于HM、AN、ME、NE的比例关系式,然后分两种情况考虑:
①当3cm的边在BN上时,可设NM为x,根据上面得到的比例线段,可求得HM的表达式,进而可表示出HG的长,HP的长易求得,然后根据(1)题的计算方法,表示出长方体纸盒的容积,即可得到关于纸盒容积和NM长的函数关系式,根据函数的性质以及自变量的取值范围,即可得到长方体纸盒的最大容积及对应的NM即BG的长;
②当6cm的边在BN上时,解法同①;
然后比较两种情况下,所得长方体纸盒的最大容积,即可确定裁剪方案.
(2)首先根据已知条件画出草图,设能够裁剪的矩形为CGHP,并延长GH交ND于M,由于HM∥AM,易证得△HME∽△ANE,可得关于HM、AN、ME、NE的比例关系式,然后分两种情况考虑:
①当3cm的边在BN上时,可设NM为x,根据上面得到的比例线段,可求得HM的表达式,进而可表示出HG的长,HP的长易求得,然后根据(1)题的计算方法,表示出长方体纸盒的容积,即可得到关于纸盒容积和NM长的函数关系式,根据函数的性质以及自变量的取值范围,即可得到长方体纸盒的最大容积及对应的NM即BG的长;
②当6cm的边在BN上时,解法同①;
然后比较两种情况下,所得长方体纸盒的最大容积,即可确定裁剪方案.
解答:解:(1)设矩形纸板的宽为xcm,则长为(x+8)cm.(1分)
根据题意,得4(x-8)(x+8-8)=512,(3分)
解得,x1=16,x2=-8(不合题意,舍去)(4分)
∴x+8=24(cm).(5分)
答:矩形纸板的长和宽分别24cm,16cm.
(2)设所裁剪的矩形是CGHP,延长GH交ND于点M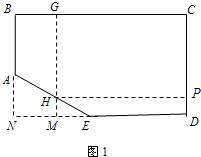
∵HM∥BN,
∴△HME∽△ANE,
∴
=
.
分两种情况:
当3cm的边在BN上时(如图1)(6分)
设NM为x,则
=
.
∴HM=3-
,∴GH=16-(3-
)=13+
;
∴V=4(13+
-8)(24-x-8)(8分)
=-2(x2-6x-160)=-2(x-3)2+338.
∴当NM为3cm时,长方体纸盒的容积最大.(9分)
当6cm的边在BN上时(如图2).(10分)
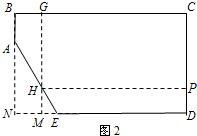 设NM为x,
设NM为x,
∴
=
,∴HM=6-2x
∴GH=16-(6-2x)=10+2x,
∴V=4(10+2x-8)(24-x-8),
=-8(x-7.5)2+578.(11分)
∵0≤x≤3,且-8<0,∴V随x增大而增大,
∴当NM为3cm时,长方体纸盒的容积最大.(12分)
综上所知,在BC上取点G,使BG=3cm,这样裁剪的矩形GHPC能使所制作的长方体纸盒的容积最大.
根据题意,得4(x-8)(x+8-8)=512,(3分)
解得,x1=16,x2=-8(不合题意,舍去)(4分)
∴x+8=24(cm).(5分)
答:矩形纸板的长和宽分别24cm,16cm.
(2)设所裁剪的矩形是CGHP,延长GH交ND于点M

∵HM∥BN,
∴△HME∽△ANE,
∴
| HM |
| AN |
| ME |
| NE |
分两种情况:
当3cm的边在BN上时(如图1)(6分)
设NM为x,则
| HM |
| 3 |
| 6-x |
| 6 |
∴HM=3-
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
∴V=4(13+
| x |
| 2 |
=-2(x2-6x-160)=-2(x-3)2+338.
∴当NM为3cm时,长方体纸盒的容积最大.(9分)
当6cm的边在BN上时(如图2).(10分)
 设NM为x,
设NM为x,∴
| HM |
| 6 |
| 3-x |
| 3 |
∴GH=16-(6-2x)=10+2x,
∴V=4(10+2x-8)(24-x-8),
=-8(x-7.5)2+578.(11分)
∵0≤x≤3,且-8<0,∴V随x增大而增大,
∴当NM为3cm时,长方体纸盒的容积最大.(12分)
综上所知,在BC上取点G,使BG=3cm,这样裁剪的矩形GHPC能使所制作的长方体纸盒的容积最大.
点评:此题考查了矩形的性质、相似三角形的判定和性质以及二次函数最值的应用;要注意的是(2)题中,3cm、6cm的边都有可能在BN上,因此要分类讨论,不要漏解.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目