题目内容
从圆外一点向半径为9的圆作切线，已知切线长为18，从这点到圆的最短距离为
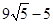
首先要根据题意作图，再作出辅助线：连接OB，即可构造直角三角形，利用勾股定理即可求得．
解：如图，
点A为圆外一点，AB切⊙O于点B，则AC是点A到⊙O的最短距离，
连接OB，则OB⊥AB，
设AC=x，则OA=9+x，
在Rt△ABO中，
∵AB2+OB2=OA2，
∴182+92=（9+x）2，
解得：x=9
-9或x=-9-9（舍去），
∴这点到圆的最短距离为9-9．
故答案为：9-9．
此题考查了切线的性质与勾股定理．连接过切点的半径是圆中的常见辅助线，要注意掌握．
解：如图，
点A为圆外一点，AB切⊙O于点B，则AC是点A到⊙O的最短距离，
连接OB，则OB⊥AB，
设AC=x，则OA=9+x，
在Rt△ABO中，
∵AB2+OB2=OA2，
∴182+92=（9+x）2，
解得：x=9
-9或x=-9-9（舍去），∴这点到圆的最短距离为9
-9．故答案为：9
-9．此题考查了切线的性质与勾股定理．连接过切点的半径是圆中的常见辅助线，要注意掌握．
练习册系列答案
名校课堂系列答案
相关题目
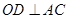于点D，连结BD、BC，
，
，则BD= 
，O），C（
