题目内容
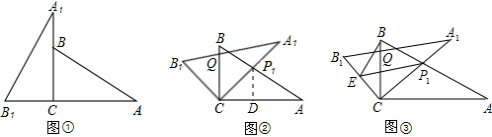
(2013•自贡)将两块全等的三角板如图①摆放,其中∠A1CB1=∠ACB=90°,∠A1=∠A=30°.
(1)将图①中的△A1B1C顺时针旋转45°得图②,点P1是A1C与AB的交点,点Q是A1B1与BC的交点,求证:CP1=CQ;
(2)在图②中,若AP1=2,则CQ等于多少?
(3)如图③,在B1C上取一点E,连接BE、P1E,设BC=1,当BE⊥P1B时,求△P1BE面积的最大值.

(1)将图①中的△A1B1C顺时针旋转45°得图②,点P1是A1C与AB的交点,点Q是A1B1与BC的交点,求证:CP1=CQ;
(2)在图②中,若AP1=2,则CQ等于多少?
(3)如图③,在B1C上取一点E,连接BE、P1E,设BC=1,当BE⊥P1B时,求△P1BE面积的最大值.

分析:(1)先判断∠B1CQ=∠BCP1=45°,利用ASA即可证明△B1CQ≌△BCP1,从而得出结论.
(2)作P1D⊥CA于D,在RtADP1中,求出P1D,在Rt△CDP1中求出CP1,继而可得出CQ的长度.
(3)证明△AP1C∽△BEC,则有AP1:BE=AC:BC=
:1,设AP1=x,则BE=
x,得出S△P1BE关于x的表达式,利用配方法求最值即可.
(2)作P1D⊥CA于D,在RtADP1中,求出P1D,在Rt△CDP1中求出CP1,继而可得出CQ的长度.
(3)证明△AP1C∽△BEC,则有AP1:BE=AC:BC=
| 3 |
| ||
| 3 |
解答:(1)证明:∵∠B1CB=45°,∠B1CA1=90°,
∴∠B1CQ=∠BCP1=45°,
∵在△B1CQ和△BCP1中,
,
∴△B1CQ≌△BCP1(ASA),
∴CQ=CP1;
(2)作P1D⊥CA于D,
∵∠A=30°,
∴P1D=
AP1=1,
∵∠P1CD=45°,
∴
=sin45°=
,
∴CP1=
P1D=
,
又∵CP1=CQ,
∴CQ=
;
(3)∵∠P1BE=90°,∠ABC=60°,
∴∠A=∠CBE=30°,
∴AC=
BC,
由旋转的性质可得:∠ACP1=∠BCE,
∴△AP1C∽△BEC,
∴AP1:BE=AC:BC=
:1,
设AP1=x,则BE=
x,
在Rt△ABC中,∠A=30°,
∴AB=2BC=2,
∴S△P1BE=
×
x(2-x)=-
x2+
x
=-
(x-1)2+
,
故当x=1时,S△P1BE(max)=
.
∴∠B1CQ=∠BCP1=45°,
∵在△B1CQ和△BCP1中,
|
∴△B1CQ≌△BCP1(ASA),
∴CQ=CP1;
(2)作P1D⊥CA于D,

∵∠A=30°,
∴P1D=
| 1 |
| 2 |
∵∠P1CD=45°,
∴
| P1D |
| CP1 |
| ||
| 2 |
∴CP1=
| 2 |
| 2 |
又∵CP1=CQ,
∴CQ=
| 2 |
(3)∵∠P1BE=90°,∠ABC=60°,
∴∠A=∠CBE=30°,
∴AC=
| 3 |
由旋转的性质可得:∠ACP1=∠BCE,
∴△AP1C∽△BEC,
∴AP1:BE=AC:BC=
| 3 |
设AP1=x,则BE=
| ||
| 3 |
在Rt△ABC中,∠A=30°,
∴AB=2BC=2,
∴S△P1BE=
| 1 |
| 2 |
| ||
| 3 |
| ||
| 6 |
| ||
| 3 |
=-
| ||
| 6 |
| ||
| 6 |
故当x=1时,S△P1BE(max)=
| ||
| 6 |
点评:本题考查了相似三角形的判定与性质,解答本题需要我们熟练掌握含30°角的直角三角形的性质、勾股定理及配方法求二次函数的最值,有一定难度.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
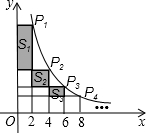 (2013•自贡)如图,在函数
(2013•自贡)如图,在函数