Question

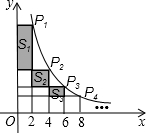（2013•自贡）如图，在函数y=

8

x

(x＞0)的图象上有点P₁、P₂、P₃…、P_n、P_n+1，点P₁的横坐标为2，且后面每个点的横坐标与它前面相邻点的横坐标的差都是2，过点P₁、P₂、P₃…、P_n、P_n+1分别作x轴、y轴的垂线段，构成若干个矩形，如图所示，将图中阴影部分的面积从左至右依次记为S₁、S₂、S₃…、S_n，则S₁=

4

，S_n=

8

n(n+1)

．（用含n的代数式表示）

Answer 1

分析：求出P₁、P₂、P₃、P₄…的纵坐标，从而可计算出S₁、S₂、S₃、S₄…的高，进而求出S₁、S₂、S₃、S₄…，从而得出S_n的值．

解答：解：当x=2时，P₁的纵坐标为4，
当x=4时，P₂的纵坐标为2，
当x=6时，P₃的纵坐标为

4

3

，
当x=8时，P₄的纵坐标为1，
当x=10时，P₅的纵坐标为：

4

5

，
…
则S₁=2×（4-2）=4=2[

8

2×1

-

8

2×(1+1)

]；
S₂=2×（2-

4

3

）=2×

2

3

=2[

8

2×2

-

8

2×(2+1)

]；
S₃=2×（

4

3

-1）=2×

1

3

=2[

8

2×3

-

8

2×(3+1)

]；
…
Sn=2[

8

2n

-

8

2(n+1)

]=

8

n(n+1)

；
故答案为：4，

8

n(n+1)

．

点评：此题考查了反比例函数图象上点的坐标特征，根据坐标求出个阴影的面积表达式是解题的关键．